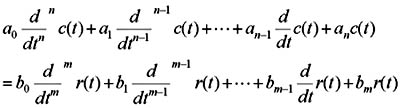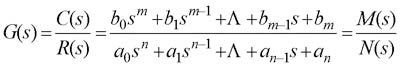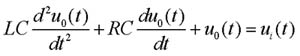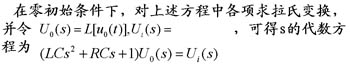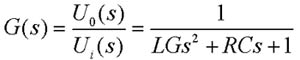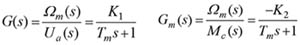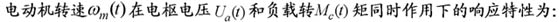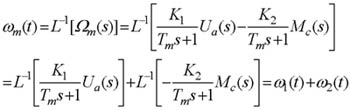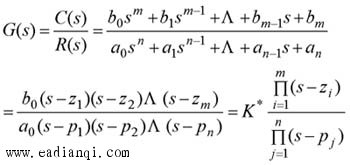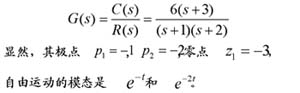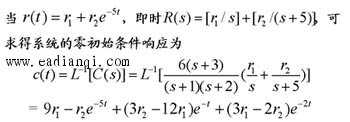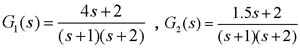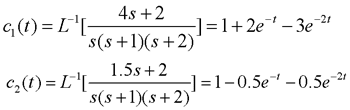复数域数学模型——传递函数
传递函数是经典控制理论中最基本和最重要的概念
频率法、根轨迹法
1、 传递函数的定义与性质
(1)定义
传递函数:在零初始条件下,系统输出量的拉氏变换与输入量的拉氏变换之比。
由n阶线性微分方程推出传递函数的方法:
在零初始条件下,由传递函数的定义得 自动控制网www.eadianqi.com版权所有
下面举例说明
例6 试求例2 RLC无源网络的传递函数 。
解 RLC网络的微分方程用式(2-1)表示为 自动控制网www.eadianqi.com版权所有
由传递函数定义,网络传递函数为: 自动控制网www.eadianqi.com版权所有
故将微分方程的算符d/dt用复数s置换便得到传递函数;反之,将传递函数多项式中的变量s用算苻d/dt置换便得微分方程。
(2)性质
1)传递函数是复变量s的有理真分式函数;
2)传递函数仅与系统自身的结构和参数有关, 与系统输入量形式无关;
3)传递函数与微分方程有相通性,可相互转换;
4)传递函数是系统单位脉冲响应的拉氏变换。 本文来自www.eadianqi.com
2、传递函数的零点和极点
(1)传递函数表示形式 本文来自www.eadianqi.com
(2)传递函数表示形式为:
< |
3.传递函数的零点和极点对输出的影响
(1)传递函数的极点可受输入函数的激发,在输出响应中形成自由运动模态。
现举例说明:
由于传递函数的极点就是微分方程的特征根,因此它们决定了所描述系统自由运动的模态,而且在强迫运动中(即零初始条件响应)也会包含这些自由运动的模态。
设某系统传递函数为 本文来自www.eadianqi.com
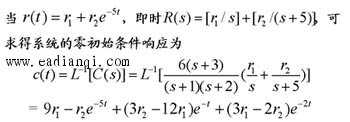 本文来自www.eadianqi.com
式中,前两项具有与输入函数r(t)相同的模态,后两项中包含了由极点-1和-2形成的自由运动模态。这是系统“固有”的成分,但其系数>却与输入函数有关,因此可以认为这两项是受输入函数激而形成的。
(2)传递函数的零点不形成自由运动模态,却影响各模态在响应中所占的比重,影响响应曲线的形状。
现举例说明:
设具有相同极点但零点不同的传递函数分别为
其极点都是-1和-2,G1(s)的零点Z1=-0.5,G2(s)的零点Z2=-1.33。
在零初始条件下,它们的价跃响应分别是
上述结果表明,模态e-t和e-2t在两个系统的单位价跃响应中所占的比重是不同的,它取决于极点之间的距离和极点与零点之间的距离,以及零点与原点之间的距离。在极点相同的情况下,G1(s) 的零点z1 接近原点,距两个极点的距离都比较远,因此,两个模态所占比重大且零点z1 的作用明显;而G2(s)的零点z2距原点较远且与两个极点均相距较近,因此两个模态所占比重就小。这样,尽管两个系统的模态相同,但由于零点的位置不同,其单位价跃响应C1(t)和C2(t)却具有不同的形状。
|