|
凡用二阶微分方程描述的系统称为二阶系统。标准形式的二阶系统的微分方程是 本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有
或 本文来自www.eadianqi.com
本文来自www.eadianqi.com
上两式中,T称为系统的时间常数。
标准形式二阶系统的闭环传递函数为 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
本文来自www.eadianqi.com 二阶系统的状态空间表达式为 本文来自www.eadianqi.com
在式(3.30)和式(3.31)中,设K=1,u(t)为输入函数。
3.3.1 二阶系统的单位跃阶响应 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 特征方程的二个根为 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有
这也是二阶系统的闭环极点。 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
下面分几种不同的情况来讨论二阶系统的单位阶跃响应。
闭环极点在s平面上的分布如图3.10所示。随 自动控制网www.eadianqi.com版权所有
响应的时域表达式为 本文来自www.eadianqi.com
这是一个等幅的正弦振荡。这说明在无阻尼状态下系统不可能跟踪单位阶跃输入的变化。 本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有
2. 欠阻尼状态(
自动控制网www.eadianqi.com版权所有
闭环极点在s平面上的分布如图3.11所示。特征方程的根具有相同的实部 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有
或 本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有 系统的单位阶跃响应为 自动控制网www.eadianqi.com版权所有
把式(3.41)展开为部分分式 自动控制网www.eadianqi.com版权所有
对式(3.42)求拉普拉斯变换,得到 本文来自www.eadianqi.com
式(3.43)还可以进一步写成: 本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有 式(3.44)表明,这是一个振幅按指数规律衰减的正弦振荡过程。图3.12是y(t)在欠阻尼情况下的响应曲线。 本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有
式(3.44)中,正弦振荡的振幅为
自动控制网www.eadianqi.com版权所有
3.临界阻尼状态( 本文来自www.eadianqi.com
本文来自www.eadianqi.com
即二阶系统具有相等的负实数闭环极点。图3.13给出了闭环极点在S平面上的分布。图中用双星号表示特征方程的重根。
自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有 对上式进行拉普拉斯反变换得: 本文来自www.eadianqi.com
其响应曲线见图3.15,在临界阻尼状态下,系统的响应开始失去振荡特性,成为单调变化的曲线。 本文来自www.eadianqi.com
4.过阻尼状态(
本文来自www.eadianqi.com 过阻尼状态下系统的单位阶跃响应为 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
对式(3.47)进行拉普拉斯反变换得 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 其响应曲线见图3.15,这是两个衰减指数项的叠加。这种情况下,二阶系统的特征方程可以改写为 本文来自www.eadianqi.com
其中 本文来自www.eadianqi.com
本文来自www.eadianqi.com 于是闭环传递函数可写为 本文来自www.eadianqi.com
式(3.49)表明,过阻尼状态下的二阶系统可以看成是两个时间常数不同的惯性环节的串联。过阻尼状态下的两个闭环极点距虚轴的距离不同。离虚轴近的闭环极点对应的(3.48)式的指数项衰减得慢,因而对输出影响大。而离虚轴远的闭环极点所对应的指数项则衰减得很快,对输出的影响较小。当 |
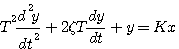 (3.27)
(3.27) 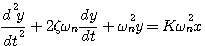 (3.28)
(3.28) 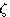 称为系统的阻尼系数或阻尼比,
称为系统的阻尼系数或阻尼比,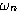 称为系统的无阻尼自然振荡频率或自然频率。K为放大系数。
称为系统的无阻尼自然振荡频率或自然频率。K为放大系数。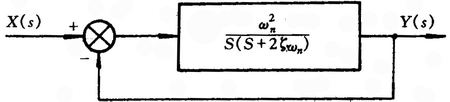
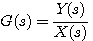
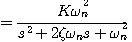 (3.29)
(3.29) 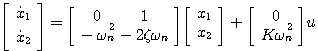 (3.30)
(3.30) 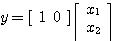 (3.31) 自动控制网www.eadianqi.com版权所有
(3.31) 自动控制网www.eadianqi.com版权所有 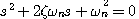 (3.32)
(3.32) 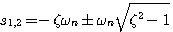 (3.33)
(3.33) 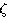 ,
,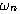 是变化的,
是变化的,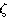 取值不同,特征方程的根(即闭环极点)可能是复数,也可能是实数。系统的响应形式也因此会有较大的区别。
取值不同,特征方程的根(即闭环极点)可能是复数,也可能是实数。系统的响应形式也因此会有较大的区别。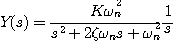 (3.34)
(3.34) 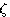 =0)
=0)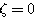 时,我们称二阶系统处于无阻尼状态或无阻尼情况。
时,我们称二阶系统处于无阻尼状态或无阻尼情况。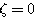 时,二阶系统特征方程的根是共轭纯虚数根 自动控制网www.eadianqi.com版权所有
时,二阶系统特征方程的根是共轭纯虚数根 自动控制网www.eadianqi.com版权所有 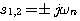
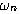 变动,闭环极点的位置沿虚轴变化。系统的单位阶跃响应为
变动,闭环极点的位置沿虚轴变化。系统的单位阶跃响应为 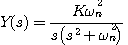 (3.35) 自动控制网www.eadianqi.com版权所有
(3.35) 自动控制网www.eadianqi.com版权所有 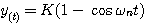 (3.36) 本文来自www.eadianqi.com
(3.36) 本文来自www.eadianqi.com 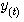 的变化曲线如图3.15所示。
的变化曲线如图3.15所示。 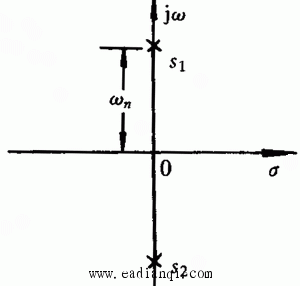
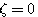 时特征根分布
时特征根分布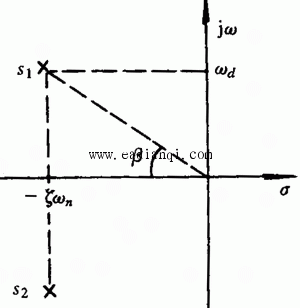
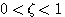 )
)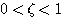 时,我们称二阶系统的单位阶跃响应是欠阻尼情况或者说二阶系统处于欠阻尼状态。
时,我们称二阶系统的单位阶跃响应是欠阻尼情况或者说二阶系统处于欠阻尼状态。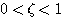 时,二阶系统特征方程的根是一对共轭复数根: 自动控制网www.eadianqi.com版权所有
时,二阶系统特征方程的根是一对共轭复数根: 自动控制网www.eadianqi.com版权所有 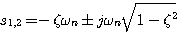 (3.37)
(3.37) 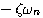 。特征方程的根的虚部为
。特征方程的根的虚部为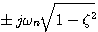 ,我们定义
,我们定义 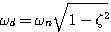 (3.38)
(3.38) 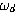 称为阻尼频率。在图3.11中,设闭环极点与s平面原点的连线和实轴的夹角为
称为阻尼频率。在图3.11中,设闭环极点与s平面原点的连线和实轴的夹角为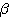 ,则有 自动控制网www.eadianqi.com版权所有
,则有 自动控制网www.eadianqi.com版权所有 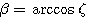 (3.39) 自动控制网www.eadianqi.com版权所有
(3.39) 自动控制网www.eadianqi.com版权所有  (3.40)
(3.40) 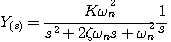 (3.41) 自动控制网www.eadianqi.com版权所有
(3.41) 自动控制网www.eadianqi.com版权所有 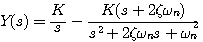
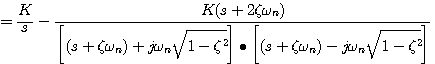 本文来自www.eadianqi.com
本文来自www.eadianqi.com 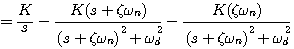 (3.42) 本文来自www.eadianqi.com
(3.42) 本文来自www.eadianqi.com 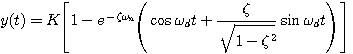 (3.43) 自动控制网www.eadianqi.com版权所有
(3.43) 自动控制网www.eadianqi.com版权所有 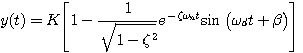 (3.44)
(3.44) 
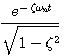 ,可以看出,若
,可以看出,若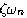 越大,振幅衰减得就越快。从图3.11闭环极点分布上,可以看出闭环极点离虚轴越远,振幅衰减得越快。
越大,振幅衰减得就越快。从图3.11闭环极点分布上,可以看出闭环极点离虚轴越远,振幅衰减得越快。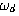 是正弦振荡的频率。图3.11表明,闭环极点离实轴越远,振荡频率就越高。欠阻尼响应随
是正弦振荡的频率。图3.11表明,闭环极点离实轴越远,振荡频率就越高。欠阻尼响应随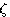 变化的曲线见图3.15。
变化的曲线见图3.15。 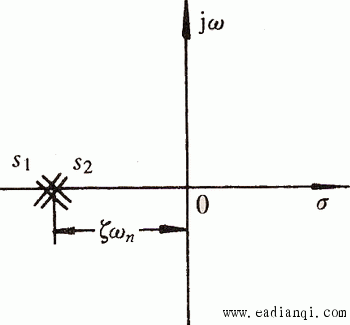
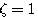 )
)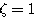 时,我们称二阶系统处于临界阻尼状态或临界阻尼情况。
时,我们称二阶系统处于临界阻尼状态或临界阻尼情况。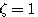 时,二阶系统的特征根为
时,二阶系统的特征根为 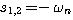
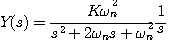
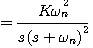
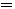
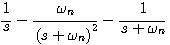 (3.45)
(3.45) 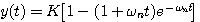 (3.46) 自动控制网www.eadianqi.com版权所有
(3.46) 自动控制网www.eadianqi.com版权所有 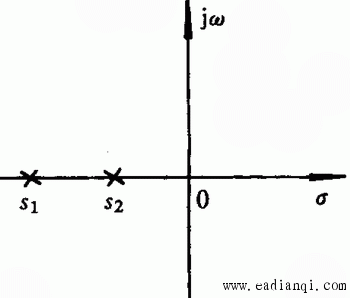
 )
)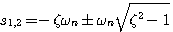
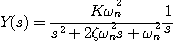
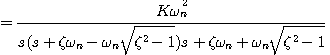
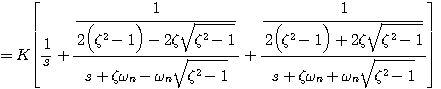 (3.47)
(3.47) 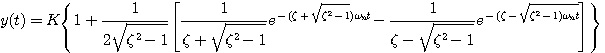
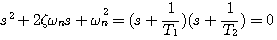 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 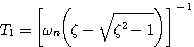 本文来自www.eadianqi.com
本文来自www.eadianqi.com 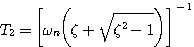
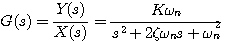 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 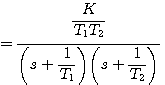 本文来自www.eadianqi.com
本文来自www.eadianqi.com 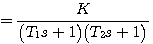 (3.49) 本文来自www.eadianqi.com
(3.49) 本文来自www.eadianqi.com