|
可用一阶微分方程描述的系统,称为一阶系统。典型的一阶系统微分方程式为 自动控制网www.eadianqi.com版权所有
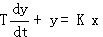 (3.7) 本文来自www.eadianqi.com (3.7) 本文来自www.eadianqi.com
系统的传递函数为 本文来自www.eadianqi.com
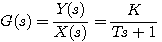 (3.8) 本文来自www.eadianqi.com (3.8) 本文来自www.eadianqi.com
式中T为系统的时间常数,K为系统的放大系数,y(t)为系统的输出变量,x(t)为系统的输入变量。 自动控制网www.eadianqi.com版权所有
3.2.1 一阶系统的单位阶跃响应
一阶系统的单位阶跃响应为 自动控制网www.eadianqi.com版权所有
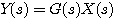 本文来自www.eadianqi.com 本文来自www.eadianqi.com
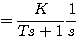 (3.9) 自动控制网www.eadianqi.com版权所有 (3.9) 自动控制网www.eadianqi.com版权所有
将式(3.9)展开为部分分式 自动控制网www.eadianqi.com版权所有
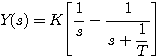 (3.10) 本文来自www.eadianqi.com (3.10) 本文来自www.eadianqi.com
对式(3.10)两边进行拉普拉斯变换,得到 自动控制网www.eadianqi.com版权所有
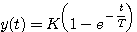 (3.11) 自动控制网www.eadianqi.com版权所有 (3.11) 自动控制网www.eadianqi.com版权所有
式(3.10)即一阶系统的单位阶跃响应。图3.4给出了响应y(t)的变化曲线:
这是一条指数曲线。在t=0时,曲线的斜率最大。 自动控制网www.eadianqi.com版权所有
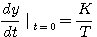 (3.12) (3.12) 本文来自www.eadianqi.com
曲线斜率随时间增加不断下降。当t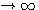 时,斜率为零,动态过程结束。这时的响应记为 时,斜率为零,动态过程结束。这时的响应记为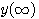 =K,即单位阶跃信号经过了一阶系统后被放大了K倍。过t=0点做响应曲线的切线,与 =K,即单位阶跃信号经过了一阶系统后被放大了K倍。过t=0点做响应曲线的切线,与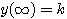 表示的直线交于P点。P点所对应的时间t=T,而此时响应值y(T)=0.632K。工程上常用这个特征来判断实验曲线是不是一阶系统的响应曲线。 本文来自www.eadianqi.com 表示的直线交于P点。P点所对应的时间t=T,而此时响应值y(T)=0.632K。工程上常用这个特征来判断实验曲线是不是一阶系统的响应曲线。 本文来自www.eadianqi.com
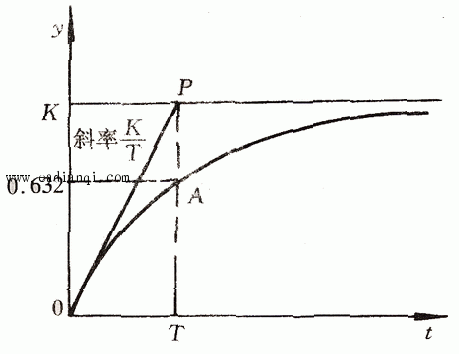
图3.4 一阶系统的单位阶跃响应 本文来自www.eadianqi.com
y(t)的瞬态响应曲线从t=0到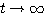 逐渐变缓。y(t)变化的几个典型值见表3.1。从表3.1可以看出,一阶系统瞬态响应的主要部分是在动态过程初始阶段内完成的。 逐渐变缓。y(t)变化的几个典型值见表3.1。从表3.1可以看出,一阶系统瞬态响应的主要部分是在动态过程初始阶段内完成的。 本文来自www.eadianqi.com
|
表3.1 一阶系统响应的典型值 本文来自www.eadianqi.com
|
|
时间t 本文来自www.eadianqi.com
|
响应y(t) 自动控制网www.eadianqi.com版权所有
|
|
t=T 本文来自www.eadianqi.com
|
y(t)=0.632K 本文来自www.eadianqi.com
|
|
t=2T 自动控制网www.eadianqi.com版权所有
|
y(t)=0.865K 自动控制网www.eadianqi.com版权所有
|
|
t=3T 本文来自www.eadianqi.com
|
y(t)=0.95K 自动控制网www.eadianqi.com版权所有
|
|
t=4T 本文来自www.eadianqi.com
|
y(t)=0.982K 自动控制网www.eadianqi.com版权所有
|
|
t=5T 本文来自www.eadianqi.com
|
y(t)=0.99K 本文来自www.eadianqi.com
|
理论上来看,只有在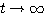 时,一阶系统的单位阶跃响应动态过程才能结束。在实际工程中,当输出响应进入到一定的误差范围后,就可以认为动态过程已经结束。我们用调节时间 时,一阶系统的单位阶跃响应动态过程才能结束。在实际工程中,当输出响应进入到一定的误差范围后,就可以认为动态过程已经结束。我们用调节时间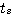 来描述动态过程的长短。 来描述动态过程的长短。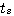 就是一个系统的动态性能指标。工业上常取的误差范围为2%或5%,若取2%的误差范围,则 就是一个系统的动态性能指标。工业上常取的误差范围为2%或5%,若取2%的误差范围,则 本文来自www.eadianqi.com
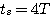 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
若取5%的误差范围,则 自动控制网www.eadianqi.com版权所有
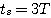 本文来自www.eadianqi.com
一阶系统的时间常数是决定系统动态特性的参数。T的大小表明了一阶系统惯性的大小。T越大,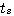 也越大,说明系统响应变化得慢。T越小,即系统惯性小, 也越大,说明系统响应变化得慢。T越小,即系统惯性小,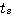 也越小,输出响应变化得就快。 自动控制网www.eadianqi.com版权所有 也越小,输出响应变化得就快。 自动控制网www.eadianqi.com版权所有
3.2.2 一阶系统的单位斜坡响应
一阶系统单位斜坡响应的拉普拉斯变换为 自动控制网www.eadianqi.com版权所有
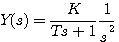 本文来自www.eadianqi.com 本文来自www.eadianqi.com
展开成部分分式后得到 自动控制网www.eadianqi.com版权所有
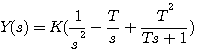 (3.14) (3.14) 自动控制网www.eadianqi.com版权所有
求(3.14)式的拉普拉斯变换,得到 自动控制网www.eadianqi.com版权所有
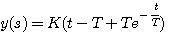 (3.15) (3.15) 自动控制网www.eadianqi.com版权所有
图3.5给出了一阶系统的单位斜坡响应曲线。从图上可以看出,即使在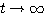 ,达到稳定状态,输出与输入之间仍有差值。 自动控制网www.eadianqi.com版权所有 ,达到稳定状态,输出与输入之间仍有差值。 自动控制网www.eadianqi.com版权所有
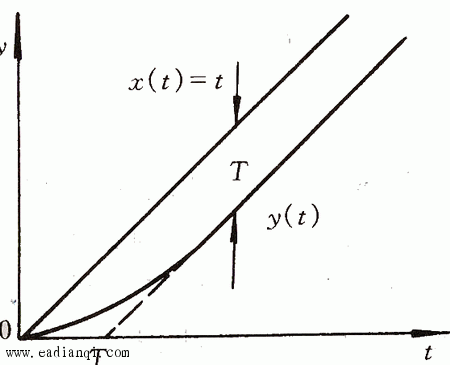
图3.5 一阶系统的单位斜坡响应 本文来自www.eadianqi.com
3.2.3 一阶系统的单位脉冲响应
由于单位脉冲函数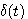 拉普拉斯变换等于1,所以一阶系统单位脉冲响应在形式上等于一阶系统的传递函数 自动控制网www.eadianqi.com版权所有 拉普拉斯变换等于1,所以一阶系统单位脉冲响应在形式上等于一阶系统的传递函数 自动控制网www.eadianqi.com版权所有
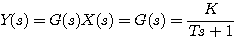 (3.16) (3.16) 本文来自www.eadianqi.com
经拉普拉斯变换后,由式(3.16)可得 本文来自www.eadianqi.com
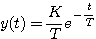 (3.17) (3.17) 本文来自www.eadianqi.com
图3.6给出了一阶系统单位脉冲响应曲线。 本文来自www.eadianqi.com
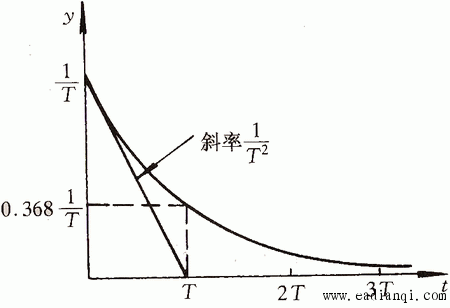
图3.6 一阶系统的单位脉冲响应 自动控制网www.eadianqi.com版权所有
3.2.4 控制系统在任意输入函数下的响应
以上我们讨论了一阶系统在几种典型信号输入下的响应。有时,我们还需要得到控制系统在任意输入函数作用下的输出响应。从式3.16可以知道,任何控制系统的单位脉冲响应实际上就是该系统传递函数G(s)的拉普拉斯反变换,记为g(t): 本文来自www.eadianqi.com
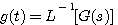 本文来自www.eadianqi.com 本文来自www.eadianqi.com
图3.7给出了一个任意形式的输入函数x(t)。我们可以用n个脉冲函数序列对x(t)进行近似表示。设第i个脉冲函数的幅度为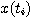 ,脉冲宽度为 ,脉冲宽度为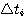 ,如图3.7所示。当脉冲宽度比系统时间常数小得多时,可以认为每一个脉冲函数就是一个理想脉冲。输入函数x(t)就是这n个理想脉冲函数的叠加。即 ,如图3.7所示。当脉冲宽度比系统时间常数小得多时,可以认为每一个脉冲函数就是一个理想脉冲。输入函数x(t)就是这n个理想脉冲函数的叠加。即 本文来自www.eadianqi.com
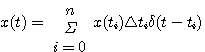 (3.18) 本文来自www.eadianqi.com (3.18) 本文来自www.eadianqi.com
式中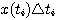 表示每个理想脉冲的强度,即每个理想脉冲包含的面积, 表示每个理想脉冲的强度,即每个理想脉冲包含的面积,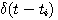 则表明了该理想脉冲发生的时刻(或时间序列)。 则表明了该理想脉冲发生的时刻(或时间序列)。
对应于第i个理想脉冲的输出是 本文来自www.eadianqi.com
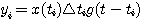 (3.19) 本文来自www.eadianqi.com (3.19) 本文来自www.eadianqi.com
因为线性系统满足叠加定理,系统的脉冲响应为 本文来自www.eadianqi.com
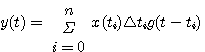 (3.20) (3.20) 自动控制网www.eadianqi.com版权所有
在3.20式中,若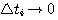 ,则系统对任意输入函数x(t)的响应就可以精确的得到 本文来自www.eadianqi.com ,则系统对任意输入函数x(t)的响应就可以精确的得到 本文来自www.eadianqi.com
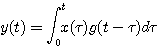 (3.21) 本文来自www.eadianqi.com (3.21) 本文来自www.eadianqi.com
式(3.21)称为函数x(t)和g(t)的卷积分,记为 本文来自www.eadianqi.com
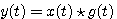 (3.22) 本文来自www.eadianqi.com (3.22) 本文来自www.eadianqi.com
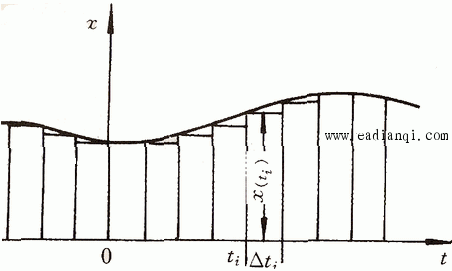
图3.7 任意形式的输入函数 自动控制网www.eadianqi.com版权所有
图3.8给出了任意输入下系统的响应曲线。 自动控制网www.eadianqi.com版权所有

图3.8 任意输入函数作用下的输出 自动控制网www.eadianqi.com版权所有
仔细观察典型的输入函数,我们会发现,对抛物线函数求导 本文来自www.eadianqi.com
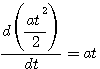 (3.23) 自动控制网www.eadianqi.com版权所有 (3.23) 自动控制网www.eadianqi.com版权所有
令a=v,则抛物线函数求导后为斜坡函数。同样,对斜坡函数求导 本文来自www.eadianqi.com
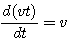 (3.24) (3.24) 自动控制网www.eadianqi.com版权所有
令v=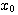 ,斜坡函数的一阶导数就是阶跃函数。而单位阶跃函数的一阶导数就是单位脉冲函数。 ,斜坡函数的一阶导数就是阶跃函数。而单位阶跃函数的一阶导数就是单位脉冲函数。
线性定常系统对典型输入信号的响应也有这种关系。一阶系统的单位脉冲响应为 自动控制网www.eadianqi.com版权所有
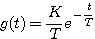 (3.25) 本文来自www.eadianqi.com (3.25) 本文来自www.eadianqi.com
对式(3.25)积分 本文来自www.eadianqi.com
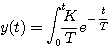 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
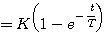 (3.26) (3.26) 自动控制网www.eadianqi.com版权所有
式(3.26)则是一阶系统的阶跃响应。
由此可以得出结论:线性定常系统对输入信号导数的响应,等于系统对该输入信号响应的导数,系统对输入信号积分的响应,等于系统对该输入信号响应的积分。这是线性定常系统的一个重要特性。我们可以根据这一特性,较方便地求出较复杂输入信号的响应。 本文来自www.eadianqi.com
|
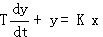 (3.7)
(3.7) 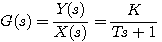 (3.8)
(3.8) 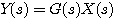 本文来自www.eadianqi.com
本文来自www.eadianqi.com 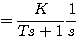 (3.9)
(3.9) 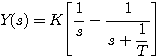 (3.10)
(3.10) 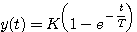 (3.11) 自动控制网www.eadianqi.com版权所有
(3.11) 自动控制网www.eadianqi.com版权所有 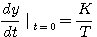 (3.12)
(3.12) 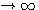 时,斜率为零,动态过程结束。这时的响应记为
时,斜率为零,动态过程结束。这时的响应记为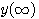 =K,即单位阶跃信号经过了一阶系统后被放大了K倍。过t=0点做响应曲线的切线,与
=K,即单位阶跃信号经过了一阶系统后被放大了K倍。过t=0点做响应曲线的切线,与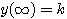 表示的直线交于P点。P点所对应的时间t=T,而此时响应值y(T)=0.632K。工程上常用这个特征来判断实验曲线是不是一阶系统的响应曲线。 本文来自www.eadianqi.com
表示的直线交于P点。P点所对应的时间t=T,而此时响应值y(T)=0.632K。工程上常用这个特征来判断实验曲线是不是一阶系统的响应曲线。 本文来自www.eadianqi.com 
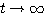 逐渐变缓。y(t)变化的几个典型值见表3.1。从表3.1可以看出,一阶系统瞬态响应的主要部分是在动态过程初始阶段内完成的。
逐渐变缓。y(t)变化的几个典型值见表3.1。从表3.1可以看出,一阶系统瞬态响应的主要部分是在动态过程初始阶段内完成的。 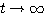 时,一阶系统的单位阶跃响应动态过程才能结束。在实际工程中,当输出响应进入到一定的误差范围后,就可以认为动态过程已经结束。我们用调节时间
时,一阶系统的单位阶跃响应动态过程才能结束。在实际工程中,当输出响应进入到一定的误差范围后,就可以认为动态过程已经结束。我们用调节时间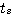 来描述动态过程的长短。
来描述动态过程的长短。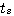 就是一个系统的动态性能指标。工业上常取的误差范围为2%或5%,若取2%的误差范围,则
就是一个系统的动态性能指标。工业上常取的误差范围为2%或5%,若取2%的误差范围,则 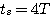
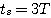
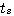 也越大,说明系统响应变化得慢。T越小,即系统惯性小,
也越大,说明系统响应变化得慢。T越小,即系统惯性小,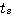 也越小,输出响应变化得就快。 自动控制网www.eadianqi.com版权所有
也越小,输出响应变化得就快。 自动控制网www.eadianqi.com版权所有 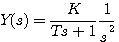 本文来自www.eadianqi.com
本文来自www.eadianqi.com 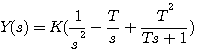 (3.14)
(3.14) 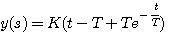 (3.15)
(3.15) 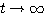 ,达到稳定状态,输出与输入之间仍有差值。 自动控制网www.eadianqi.com版权所有
,达到稳定状态,输出与输入之间仍有差值。 自动控制网www.eadianqi.com版权所有 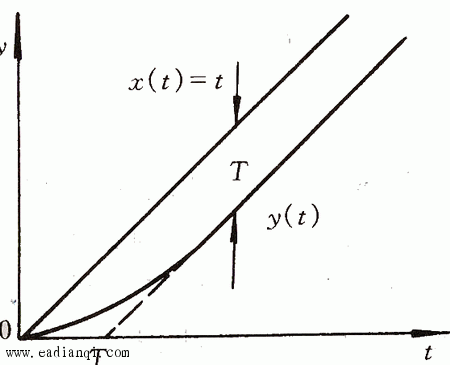
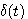 拉普拉斯变换等于1,所以一阶系统单位脉冲响应在形式上等于一阶系统的传递函数
拉普拉斯变换等于1,所以一阶系统单位脉冲响应在形式上等于一阶系统的传递函数 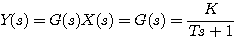 (3.16)
(3.16) 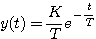 (3.17)
(3.17) 
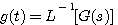
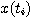 ,脉冲宽度为
,脉冲宽度为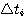 ,如图3.7所示。当脉冲宽度比系统时间常数小得多时,可以认为每一个脉冲函数就是一个理想脉冲。输入函数x(t)就是这n个理想脉冲函数的叠加。即
,如图3.7所示。当脉冲宽度比系统时间常数小得多时,可以认为每一个脉冲函数就是一个理想脉冲。输入函数x(t)就是这n个理想脉冲函数的叠加。即 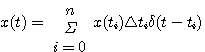 (3.18)
(3.18) 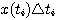 表示每个理想脉冲的强度,即每个理想脉冲包含的面积,
表示每个理想脉冲的强度,即每个理想脉冲包含的面积,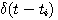 则表明了该理想脉冲发生的时刻(或时间序列)。
则表明了该理想脉冲发生的时刻(或时间序列)。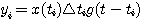 (3.19)
(3.19) 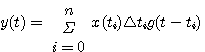 (3.20)
(3.20) 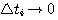 ,则系统对任意输入函数x(t)的响应就可以精确的得到 本文来自www.eadianqi.com
,则系统对任意输入函数x(t)的响应就可以精确的得到 本文来自www.eadianqi.com 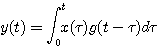 (3.21) 本文来自www.eadianqi.com
(3.21) 本文来自www.eadianqi.com 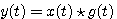 (3.22) 本文来自www.eadianqi.com
(3.22) 本文来自www.eadianqi.com 

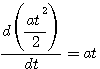 (3.23) 自动控制网www.eadianqi.com版权所有
(3.23) 自动控制网www.eadianqi.com版权所有 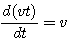 (3.24)
(3.24) 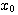 ,斜坡函数的一阶导数就是阶跃函数。而单位阶跃函数的一阶导数就是单位脉冲函数。
,斜坡函数的一阶导数就是阶跃函数。而单位阶跃函数的一阶导数就是单位脉冲函数。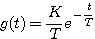 (3.25) 本文来自www.eadianqi.com
(3.25) 本文来自www.eadianqi.com 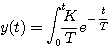 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 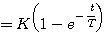 (3.26)
(3.26)