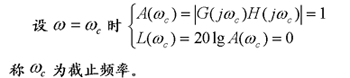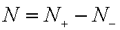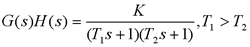|
(1)穿越点确定
对于复平面的负实轴和开环对数相频特性,当取频率为穿越频率ω时ψ(ωx)=(2k+1)π,k\0,+/-1,...设半对数坐标下ΓGH的对数幅频曲线和对数相频曲线分别为ΓL和Γψ,由于ΓL等于曲线Γ(ω),则ΓGH在A(ω)>1时,穿越负实轴的点等于ΓGH在半对数坐标下,对数幅频特性L(ω)>0时对数相频特性曲线Γψ与(2k+1)π,k=0,+/-1,L,平行线的交点。 自动控制网www.eadianqi.com版权所有
对应地,需从对数相频特性曲线ψ(ωn-)点起向上补作V1*180°的虚直线至ψ(ωn+)处,ψ(ω)曲线和补作的虚直线构成Γψ 。 本文来自www.eadianqi.com 注意:补作的虚直线所产生的穿越皆为负穿越。 对数频率稳定判据设P为开环系统正实部的极点数,反馈控制系统稳定的充分必要条件是ψ(ωc)≠(2K+1)π,k=0,1,2,L和L(ω)>0时,Γψ曲线穿越(2K+1)π 线的次数 本文来自www.eadianqi.com
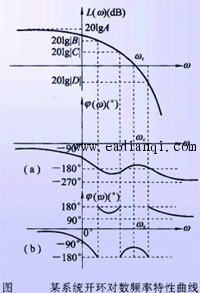
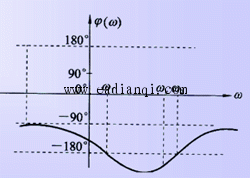
对数频率稳定判据和奈氏判据本质相同,其区别仅在于前者在L(ω)>0的频率范围内依Γψ曲线确定穿越次数N。 2)、举例 例5-10 已知某系统开环稳定,开环幅相曲线如图所示,试将开环幅相曲线表示为开环对数频率特性曲线,并运用对数稳定判据判断系统的闭环稳定性。 解:系统开环对数频率特性曲线如图所示,然而相角具有不惟一性,图中(a)和(b)为其中的两种形式。 因为开环系统稳定,P=。由开环幅相曲线知V=0,不需补作虚直线。
解 因为V=3,需在低频处由ψ(ω)曲线向上补作270°的虚直线于180°,如图所示。 知N_=1.5,N+=0,按对数稳定判据 Z=P-2N=3,故闭环不稳定极点的个数为3。
由于开环系统稳定,即P=0,因而该闭环系统稳定的充要条件是:在L(ω)≥0dB的频域内,相频特性ψ(ω)不穿越-180°线,或正、负穿越数之差为零。由图可见在L(ω)≥0的频域内ψ(ω)总大于-180°,故闭环系统是稳定的。 自动控制网www.eadianqi.com版权所有
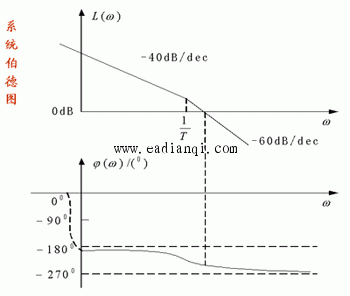
该系统开环传递函数含有2个积分环节,且ω由0->0+时,ψ(ω)由0°->180°,用虚线绘出相频特性的增补部分。由图知L(ω)>0dB的频段上, N+=0,N-=1,R =-2,而P =0,则Z=2,闭环系统不稳定。
通过前面例子分析可知,若开环传递函数在开右半s平面的极点数P=0,当开环传递函数的某些系数(如开环增益)改变时,闭环系统的稳定性将发生变化。这种闭环稳定有条件的系统,称为条件稳定系统。 相应地,无论开环传递函数的系数怎样变化,系统总是不稳定的,这样的系统称为结构不稳定系统。 |