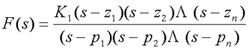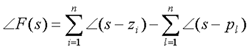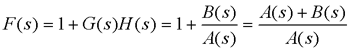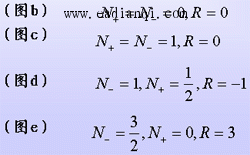|
1932年,乃奎斯特(Nyquist)提出了另一种判定闭环系统稳定性的方法,称为乃奎斯特稳定判据,简称乃氏判据。这个判据的主要特点是利用开环频率特性判定闭环系统的稳定性。此外,乃氏稳定判据还能够指出稳定的程度,揭示改善系统稳定性的方法。因此,乃氏稳定判据在频率域控制理论中有着重要的地位。 1)、辐角原理 设s为复数变量,F(s)为s 的有理分式函数,且有
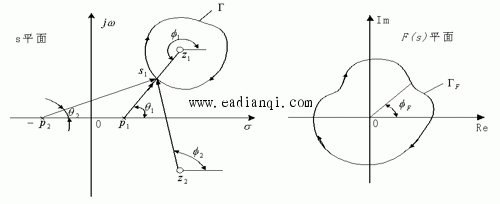
由复变函数理论知道,在s平面上任选一条闭合曲线Γ,且不通过F(s)的任一零点和极点,s从闭合曲线Γ上任一点A起,顺时针沿Γ运动一周,再回到A点,则对应F(s)的平面上亦从F(a)点起,到F(a)点止形成一条闭合曲线ΓF 。 复变函数的相角为
自动控制网www.eadianqi.com版权所有 若s平面上闭合曲线Γ以顺时针方向包围的Z个零点,则在F(s)平面上的映射曲线ΓF将按顺时针方向围绕着坐标原点旋转Z周。 若s平面上的闭合曲线Γ以顺时针方向围绕着的P个极点旋转一周,则其在平面上的映射曲线ΓF将按逆时针方向围绕坐标原点旋转P周。见下张图示。
由此可得幅角原理:设s平面闭合曲线Γ包围的Z 个零点和P个极点,则s沿Γ顺时针运动一周时,在F(s)平面上,闭合曲线ΓF包围原点的圈数为:R = P - Z R < 0和 R > 0分别表示ΓF 顺时针包围和逆时针包围 F(s) 平面的原点,R = 0表示不包围平面的原点。 2)、复变函数的选择 选择
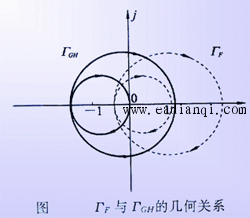
F(s)具有以下特点: (1)F(s)的零点为闭环传递函数的极点,F(s)的极点为开环传递函数的极点; (2)因为开环传递函数分母多项式的阶次一般大于或等于分子多项式的阶次,故F(s)的零点和极点数相同; (3)s沿闭合曲线 运动一周所产生的两条闭合曲线ΓF和ΓGH只相差常数1,即闭合曲线ΓF可由ΓGH沿实轴正方向平移一个单位长度获得。 图
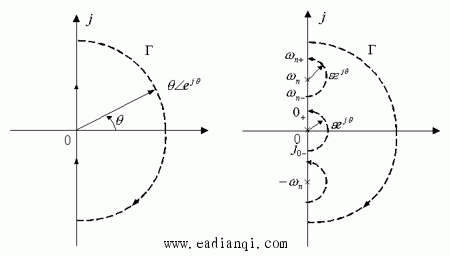
系统的闭环稳定性取决于系统闭环传递函数极点,即F(s)的零点的位置,因此当选择s平面闭合曲线Γ包围s平面的右半平面时,若Z = 0,即闭环特征根均位于左半s平面,则闭环系统稳定。考虑到前述闭合曲线Γ应不通过F(s)的零点和极点的要求,Γ可取下图所示的两种形式。
本文来自www.eadianqi.com
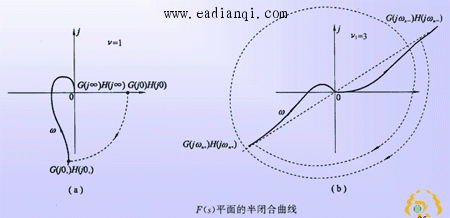
4)、 G(s)H(s)闭合曲线的绘制 (1)若G(s)H(s)无虚轴上极点
自动控制网www.eadianqi.com版权所有
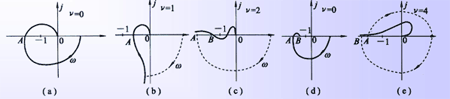
根据半闭合曲线ΓGH可获得ΓF包围原点的圈数R。设N为ΓGH穿越(-1,j0)点左侧负实轴的次数,N+表示正穿越的次数和(从上向下穿越),N-表示负穿越的次数和(从下向上穿越),则R=2N=-2(N+-N_) 在图中,虚线为按系统型次V或等幅振荡环节数V1补作的圆弧,点A,B为奈氏曲线与负实轴的交点,按穿越负 实轴上(-∞,-1) 段的方向,分别有: (图a)N-=1,N+=0,R=-2N_=-2
|