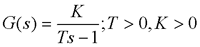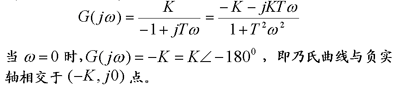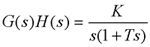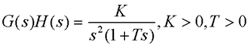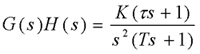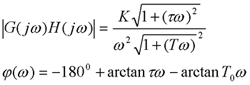奈氏判据 反馈控制系统稳定的充分必要条件是半闭合曲线ΓGH不穿过(-1,j0)点且逆时针包围临界点(-1,j0)点的圈数R等于开环传递函数的正实部极点数P。
由幅角原理可知,闭合曲线Γ包围函数 F(s)=1+G(s)H(s) 的零点数即反馈控制系统正实部极点数为
Z=P-R=P-2N 当P≠R 时,Z≠0 ,系统闭环不稳定。
当半闭合曲线ΓGH穿过(-1,j0)点时,系统可能临界稳定。
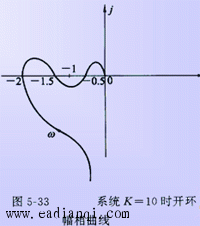
例5-8 已知单位反馈系统开环幅相曲线如图所示,试确定系统闭环稳定时K值的范围。
解: 如图所示,开环幅相曲线与负实轴有三个交点,设交点处穿越频率分别为ω1,ω2,ω3,
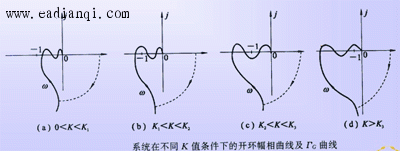
对应地,分别取0<K<K1,K1<K<K2,K2<K<K3和K>K3时,开环幅相曲线分别如图所示,图中按V补作虚圆 本文来自www.eadianqi.com
弧得半闭合曲线ΓG.
例:系统的开环传递函数为
试用乃氏判据判别闭环系统的稳定性。
解:系统开环传递函数在s的右半平面上没有任何极点,即P =0。当ω-∞->+∞变化时, 曲线如左图所示。 由图可知R = 0,所以Z = P - R = 0。这表示对于任意正值K、T1和T2,该闭环系统总是稳定的。 本文来自www.eadianqi.com
试用乃氏判据确定使该闭环系统稳定的K值范围。
解:开环系统频率特性为
系统开环系统幅频和相频特性的表达式分别为
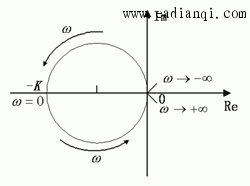
由于系统的P = 1,当ω由-∞-〉+∞变化时, G(jω)曲线如按逆时针方向围绕(-1,j0)点旋转一周,即R = 1,则Z =P-R =0,表示闭环系统是稳定的。显然,系统稳定时T > 0且K > 1。 本文来自www.eadianqi.com
例 某反馈控制系统的开环传递函数为
其中K >0,T >0。试判别该闭环系统的稳定性。
解:由于该系统为Ⅰ型系统,它在坐标原点处有一个开环极点。该图逆时针围绕原点的半径为ε的半圆,在GH平面上的映射曲线为一半径无穷大的半圆,它与乃氏曲线G(jω)H(jω)相连接后的闭合曲线如上张图所示。由图可见,R=0,而开环系统P=0,因而Z=0,即闭环系统是稳定的。
例:已知系统的开环传递函数为 本文来自www.eadianqi.com
试用乃氏稳定判据判别该闭环系统的稳定性。
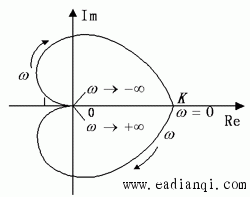
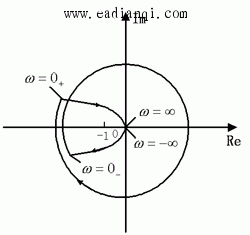
解: 由于开环传递函数在坐标原点处有重极点,由上述的讨论可知,逆时针围绕原点的半径为ω的半圆在GH平面上的映射曲线为一半径无穷大的圆,它与乃氏曲线G(jω)H(jω)相连接后的闭合曲线如下张图所示。 本文来自www.eadianqi.com
由图可见,不论K值的大小如何,乃氏曲线总是以顺时针方向围绕点(-1,j0)旋转两周,即R=-2。由于开环系统P=0,所以Z=2,表示该闭环系统总是不稳定的,且其在s的右半平面上有2个极点。
例 已知系统的开环传递函数为 本文来自www.eadianqi.com
试分析T>τ和T<τ时系统的稳定性,并画出它们所对应的乃氏图。
解:系统开环频率特性为 自动控制网www.eadianqi.com版权所有
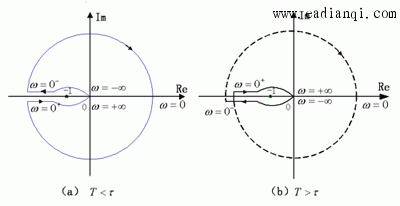
作出在T>τ和T<τ二种情况下的曲线,如下图所示。 自动控制网www.eadianqi.com版权所有
由于P=0,当T<τ时,G(jω)H(jω)曲线不包围点(-1,j0),因而闭环系统是稳定的;
当T>τ时,G(jω)H(jω)曲线以顺时针方向包围点(-1,j0)旋转二周,这意味着有两个闭环极点位于s 的右半平面上,该闭环系统不稳定。
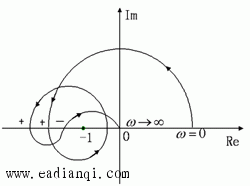
例 系统开环传递函数有2个正实部极点,开环乃氏图如下图所示,试问闭环系统是否稳定? 本文来自www.eadianqi.com
解: P=2,ω由0->∞时,由乃氏图知N+=2,N_=1,
R =2N
= 2(N+-N_ )
=2
则Z=P-R=0,闭环系统稳定。
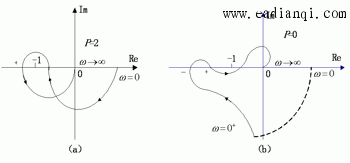
例 系统开环乃氏图如下图所示,P为开环正实部极点个数,试判定闭环系统的稳定性。 本文来自www.eadianqi.com
解:当ω由0->∞时,图a中N+=1,N-=0,R =2,而P =2,则Z=0,闭环系统稳定。图b中,N+=1,N-=1,R =0,而P =0,则Z=0,闭环系统稳定。
3 对数频率稳定判据
1)、对数频率稳定判据
可以推广运用奈氏判据,其关键问题是需要根据半对数坐标下的ΓGH曲线确定穿越次数N或N+和N-。
开环幅相曲线和开环系统存在积分环节和等幅振荡环节时所补作的半径为无穷大的虚圆弧。N 的确定取决于A(ω)>1时ΓGH穿越负实轴的次数,建立如下对应关系:
|