（1）F(s)的收敛域在S平面由平行于jω轴的带状区域所组成的。这一性质来自于这样一个事实：F(s)的ROC是由这样一些s=σ+jw所组成，在那里的傅立叶变换收敛，也就是说，f(t)的拉氏变换的ROC是由这样一些s值组成的，对于这些s值，是绝对可积的，即：，因为这个条件只与σ，即s的实部有关，故得到性质1； 自动控制网www.eadianqi.com版权所有

（2）对于有理拉氏变换来说，收敛域不包含任何极点； 因为在一个极点处，F(s)为无限大，拉氏变换的积分公式显然在极点处不收敛，所以收敛域内不包含属于极点的s值；

本文来自www.eadianqi.com

（3）如果f(t)是有限持续期，并且是绝对可积，那么收敛域就是整个s平面；

本文来自www.eadianqi.com

（4）如果f(t)是右边信号，其收敛域在最右边极点的右半平面； 本文来自www.eadianqi.com

（5）如果f(t)是左边信号，其收敛域在最左边极点的左半平面； 本文来自www.eadianqi.com

（6）若f(t)是双边信号，即无始无终信号，则其收敛域是由s平面的一条带状区域组成； 本文来自www.eadianqi.com

例：设信号f(t)为： 自动控制网www.eadianqi.com版权所有

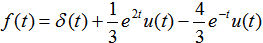
则 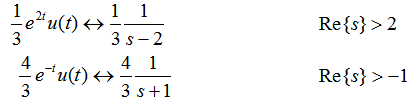本文来自www.eadianqi.com

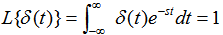　　，即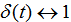： ，该结果对于任何s都是成立的，故其ROC为整个s平面。 本文来自www.eadianqi.com