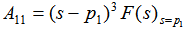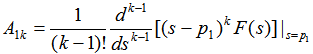|
设F(s)是有理函数,如果分子多项式的次数高于分母,就不能直接应用部分分式展开法。先做长除法,得到商和余数,先将商求其反变换,其为冲击函数及冲击函数的各阶导数。余数为部分分式展开的对象。下面讨论F(s)为真分数的情况: 本文来自www.eadianqi.com
设有理函数 本文来自www.eadianqi.com
部分分式展开的第一步是把分母N(s)进行因式分解,然后区分极点的类型,选择求取待定系数的方法。下面分别讨论极点为实数、共轭复数和多重根的三种情形: 自动控制网www.eadianqi.com版权所有 (1)极点为实数且无重根 本文来自www.eadianqi.com 设p1,p2,……pn为F(s)的实极点,则F(s)可作如下分解: 自动控制网www.eadianqi.com版权所有
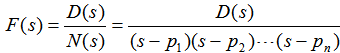 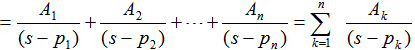 则其中待定系数的求取可以通过公式: 本文来自www.eadianqi.com 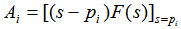 i=1、2、3、…、n i=1、2、3、…、n
或
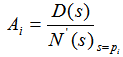 i=1、2、3、…、n i=1、2、3、…、n(2)极点为共轭复数且无重根 本文来自www.eadianqi.com 如果多项式N(s)=0具有复根,则F(s)具有复数极点,则必定以共轭形式成对出现。相应当部分分式展开的系数为共轭复数。 本文来自www.eadianqi.com
若
则 本文来自www.eadianqi.com
由于F(s)是实系数多项式之比,故A1、A2为共轭复数。 自动控制网www.eadianqi.com版权所有
设,
则:
(3)二阶和高阶极点 如果N(s)=0具有重根,则应含有 自动控制网www.eadianqi.com版权所有 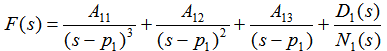 为了确定A11、A12、A13 ,可以将上式左右两边都乘以,即: 自动控制网www.eadianqi.com版权所有 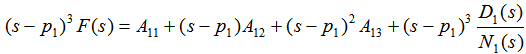
则 自动控制网www.eadianqi.com版权所有
然后将上式两边对s求导一次,A12被分离出来,即:
同理: 自动控制网www.eadianqi.com版权所有
从以上分析过程可以推论得出当N(s)=0有r重根,其余为单根的分解式为: 本文来自www.eadianqi.com
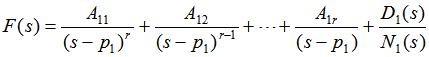
则 |
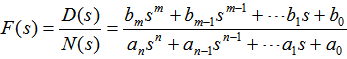
 本文来自www.eadianqi.com
本文来自www.eadianqi.com 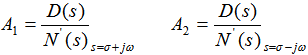
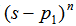 的因式。现设N(s)中含有
的因式。现设N(s)中含有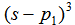 的因式,设p1为N(s)=0的三重根,其余为单根,则:
的因式,设p1为N(s)=0的三重根,其余为单根,则: