|
Roth-Hurwitz稳定判据是判别系统特征根分布的一个代数判据。
Hurwitz稳定判据(1895年提出)
系统的特征方程式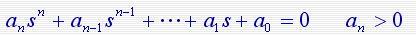
系统稳定的充要条件:
1)系统特征方程式的各项系数全部为正值,即ai>0 ( i= 0, 1, 2, …, n )。
2)由各项系数组成的Hurwitz n阶行列式中各阶子行列式 都大于零。 都大于零。
满足这两个条件的系统是稳定的系统,否则系统是不稳定的。
其中Hurwitz 行列式为 本文来自www.eadianqi.com

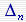 是按下列规则建立的:首先,在主对角线上从an-1开始依次写进特征方程的系数,直写到a0为止;然后,由主对角线上的系数出发,写出 是按下列规则建立的:首先,在主对角线上从an-1开始依次写进特征方程的系数,直写到a0为止;然后,由主对角线上的系数出发,写出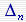 中每一列的各元素,每列由上到下系数a的脚标递增,由下到上a的脚标递减。当写到特征方程中不存在的系数时以零代替。 中每一列的各元素,每列由上到下系数a的脚标递增,由下到上a的脚标递减。当写到特征方程中不存在的系数时以零代替。
例题5-1: 系统的特征方程为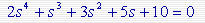
试用Hurwitz判据判别系统的稳定性。
解:由特征方程知各项系数为
a4=2, a3=1, a2=3, a1=5, a0=10
均为正值。满足判据的必要条件ai>0,再检查第二个条件。写出Hurwitz行列式: 自动控制网www.eadianqi.com版权所有

由于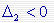 ,不满足Hurwitz行列式全部为正的条件,因此,系统不稳定。 ,不满足Hurwitz行列式全部为正的条件,因此,系统不稳定。
例题5-2:单位反馈系统的开环传递函数为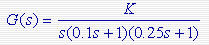 试求使系统稳定的K值范围。 试求使系统稳定的K值范围。
解:系统闭环特征方程为 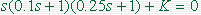
特征方程各项系数为a3=0.025, a2=0.35, a1=1, a0=K
根据Hurwitz判据,应满足下列条件:
1)ai>0,则 K>0;
2)检查 ,即 自动控制网www.eadianqi.com版权所有 ,即 自动控制网www.eadianqi.com版权所有

则 K<14。
要保证系统稳定的K值范围是 0<K<14。
从上例可以得出:K值越大,系统的稳定性越差,当K值超过一定范围,系统会变得不稳定。
Routh稳定判据(1884年提出)
系统特征方程的阶次越高,当利用Hurwitz判据时,其计算行列式的工作量越大,对于高阶系统,可采用Routh判据来判别系统的稳定性。其步骤为
1. 列出系统的特征方程式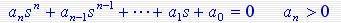
各项系数均为实数。检查各项系数是否都大于零,若都大于零,则进行第二步。
2. 按系统的特征方程式列写Routh表: 本文来自www.eadianqi.com
  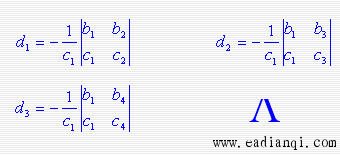 自动控制网www.eadianqi.com版权所有
计算上述各式的规律是:自s n-2行以下,每行的数都是由该行上边两行的数算得,等号右边的二阶行列式中,第一列都是上两行中第一列的两个数,第二列是被算数右上肩的两个数,等号右边的分母是上一行中左起第一个数。
由Routh表可以看出:Routh判据和Hurwitz判据实质上是相同的。Routh表中第一列各数的至和Hurwitz行列式之间的关系: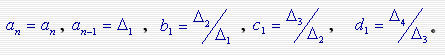
3.考察表中第一列各数的符号:
若第一列各数均为正数,则闭环特征方程所有根具有负实部,系统稳定。
如果第一列中有负数,则系统不稳定,第一列中数值符号的改变次数等于系统特征方程含有正实部根的数目。
例题5-3: 系统的特征方程为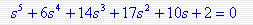
试用Routh判据确定系统是否稳定。
解:1) ai>0;
2) 列出Routh表(下边列出两个表,左表是为了和原Routh表的形式对照,右表是为了数值计算方便,二者对判断系统稳定性的作用是一样的)。 本文来自www.eadianqi.com

由于Routh表中第一列数值全部为正实数, 所以系统是稳定的。
例题5-4:已知系统的特征方程为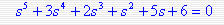
判断系统的稳定性。
解:1) ai>0;
2) 列出Routh表 本文来自www.eadianqi.com

在Routh表中第一行的数值符号的变化,数值在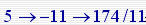 处发生了两次改变,所以系统不稳定,且特征方程有两个正根。 处发生了两次改变,所以系统不稳定,且特征方程有两个正根。 本文来自www.eadianqi.com
|
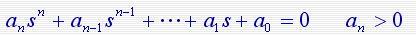
 都大于零。
都大于零。
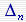 是按下列规则建立的:首先,在主对角线上从an-1开始依次写进特征方程的系数,直写到a0为止;然后,由主对角线上的系数出发,写出
是按下列规则建立的:首先,在主对角线上从an-1开始依次写进特征方程的系数,直写到a0为止;然后,由主对角线上的系数出发,写出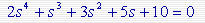

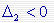 ,不满足Hurwitz行列式全部为正的条件,因此,系统不稳定。
,不满足Hurwitz行列式全部为正的条件,因此,系统不稳定。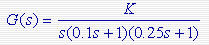 试求使系统稳定的K值范围。
试求使系统稳定的K值范围。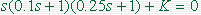
 ,即 自动控制网www.eadianqi.com版权所有
,即 自动控制网www.eadianqi.com版权所有 
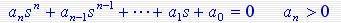


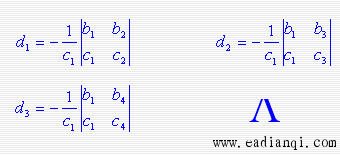
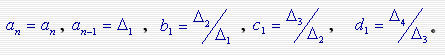

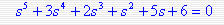

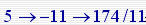 处发生了两次改变,所以系统不稳定,且特征方程有两个正根。
处发生了两次改变,所以系统不稳定,且特征方程有两个正根。