|
Roth-Hurwitz稳定判据和Nyquist稳定判据虽然能定性地判断系统的稳定性,但却不能定量地判定系统的稳定程度,本章介绍的稳定性裕量正是解决这一定量问题。如下图所示,图中画出了系统的Nyquist图和与之对应的阶跃响应曲线。 本文来自www.eadianqi.com
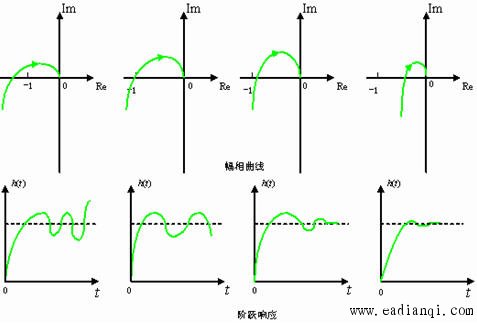
从图中的阶跃响应曲线中可以看出:系统分别处于不稳定、临界稳定核稳定状态。对于两个处于稳定状态的系统,其稳定性程度如何,却不能明确表示出来。
1. 相位裕量和幅值裕量
系统开环Nyquist曲线对(-1,j0)点的靠近程度,直接反映了系统的稳定程度。即 曲线离(-1,j0)点越远,系统的稳定程度越高,相反,曲线越靠近(-1,j0)点,系统的稳定程度越低。这就是系统的相对稳定性。 曲线离(-1,j0)点越远,系统的稳定程度越高,相反,曲线越靠近(-1,j0)点,系统的稳定程度越低。这就是系统的相对稳定性。
系统的相对稳定性是用幅值裕量和相位裕量来定量分析和计算的。 本文来自www.eadianqi.com
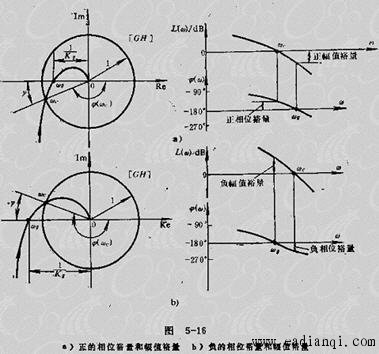
幅值交界频率: 曲线与单位圆相交时的频率 曲线与单位圆相交时的频率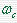 。 。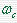 也称为幅值穿越频率和开环截止频率、开环剪切频率。 也称为幅值穿越频率和开环截止频率、开环剪切频率。
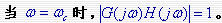 Bode图上 Bode图上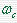 是对数幅频特性曲线与 0dB 线相交的频率。 是对数幅频特性曲线与 0dB 线相交的频率。
相位交界频率: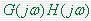 曲线与负实轴相交时的频率 曲线与负实轴相交时的频率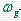 。 。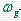 也称为相位穿越频率。 也称为相位穿越频率。 本文来自www.eadianqi.com
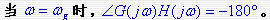 此时开环Nyquist曲线与负实轴相交。对数幅频特性曲线在 此时开环Nyquist曲线与负实轴相交。对数幅频特性曲线在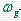 处穿越 处穿越 线。 线。
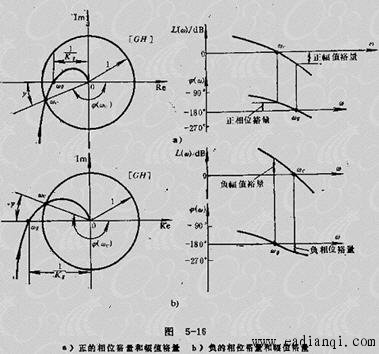
相位裕量:当 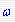 为幅值交界频率 为幅值交界频率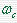 时,相频特性距 线的相位差值。用 时,相频特性距 线的相位差值。用 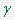 表示。即 表示。即
它表明了在幅值交界频率 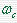 上,使系统达到不稳定边缘所需的附加相位滞后量。如图所示 自动控制网www.eadianqi.com版权所有 上,使系统达到不稳定边缘所需的附加相位滞后量。如图所示 自动控制网www.eadianqi.com版权所有
当 >0 时,系统稳定;当 >0 时,系统稳定;当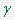 <0 ,则系统不稳定。 <0 ,则系统不稳定。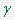 越小,系统的稳定性越差,一般取 越小,系统的稳定性越差,一般取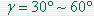 为宜, 过大,则系统灵敏度降低。 为宜, 过大,则系统灵敏度降低。
具有正相位裕量的系统不仅稳定,而且还有相当的稳定储备,它可以在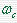 的频率下,允许相位再增加 的频率下,允许相位再增加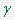 角度才达到临界稳定条件,因此相位裕量也称为相位储备。 角度才达到临界稳定条件,因此相位裕量也称为相位储备。
幅值裕量:当 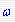 为相位交界频率 为相位交界频率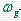 时,开环幅频特性 时,开环幅频特性 的倒数。用Kg表示,即 的倒数。用Kg表示,即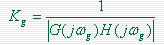 本文来自www.eadianqi.com 本文来自www.eadianqi.com
在Nyquist图上 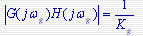
它表示了在 频率下,开环频率特性的模。如图所示 本文来自www.eadianqi.com 频率下,开环频率特性的模。如图所示 本文来自www.eadianqi.com
对于稳定系统 
对于不稳定系统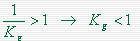
在Bode图上 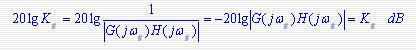
对于稳定系统 Kg(dB)必须在 0dB 线以下, Kg(dB)>0,为正幅值裕量。
对于不稳定系统 Kg(dB)必须在 0dB 线以上, Kg(dB)<0,为负幅值裕量。
如图所示 自动控制网www.eadianqi.com版权所有
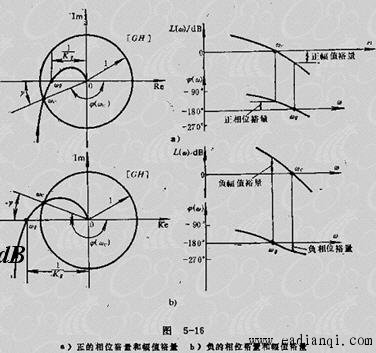
通常取 Kg(dB)> 6 dB
2. 相位裕量与时间响应的关系
二阶系统的开环传递函数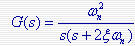 ,幅频特性 ,幅频特性 幅频特性 幅频特性 本文来自www.eadianqi.com
的幅值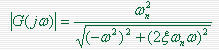 ,令 ,令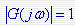 ,此时的频率幅值交界频率 ,此时的频率幅值交界频率 本文来自www.eadianqi.com
 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
 本文来自www.eadianqi.com 本文来自www.eadianqi.com
|





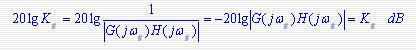

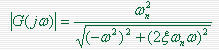 ,令
,令