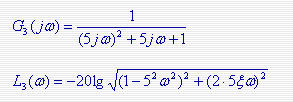|
 自动控制网www.eadianqi.com版权所有
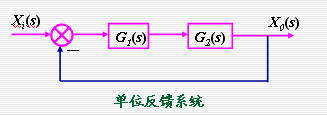
上图所示系统的开环传递函数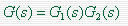 其频率特性 其频率特性 本文来自www.eadianqi.com 本文来自www.eadianqi.com
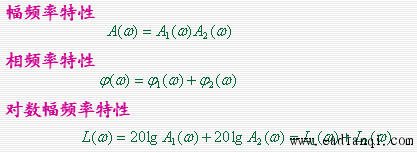
从上式可以看出:系统的对数幅频特性与对数相频特性是组成系统的各个典型环节的对数幅频特性与对数相频特性的叠加,因此,容易由典型环节的Bode图生成系统的Bode图,这也是Bode图比Nyquist图优越的地方。
但是,对于闭环系统的传递函数,当环节较多时不易写出各因式相乘的形式,用上述方法做高阶系统的闭环Bode图是困难的。
1. 绘制开环系统对数频率特性曲线的一般步骤
例题4-3:绘制图4-17所示系统的Bode图 本文来自www.eadianqi.com

解:1)将系统的传递函数转化为若干个典型环节的传递函数(标准形式,即典型环节传递函数中的常数项化成相乘的形式;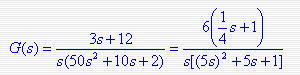 上式将系统的传递函数化为比例、积分、振荡、一阶微分四个环节组成。 上式将系统的传递函数化为比例、积分、振荡、一阶微分四个环节组成。
2)确定系统的开环频率特性,并保留各环节相乘的形式;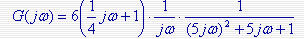
3)确定典型环节的特征参数(如:比例系数、转折频率、无阻尼固有频率等),以便确定它们的渐近线;
对于放大环节: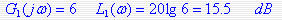
是一条水平线,无转折频率,相角为0度,如图所示(用红线示出)
对于积分环节: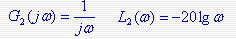
是一条过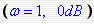 点的直线,其斜率为 点的直线,其斜率为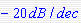 ,简写为[-20],无转折频率,相角为-90度 ,如图所示(用红线示出) ,简写为[-20],无转折频率,相角为-90度 ,如图所示(用红线示出) 自动控制网www.eadianqi.com版权所有
对于振荡环节: 自动控制网www.eadianqi.com版权所有
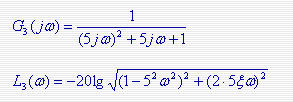
对于一阶微分环节: 自动控制网www.eadianqi.com版权所有
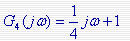
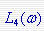 的两条渐近线为 0dB 线和斜率为[+20]的直线,转折频率4 ,相频 由0度到90度 。在转折频率w2=4 处的相角为45度 ,如图所示(用黄线示出) 的两条渐近线为 0dB 线和斜率为[+20]的直线,转折频率4 ,相频 由0度到90度 。在转折频率w2=4 处的相角为45度 ,如图所示(用黄线示出)
4)选定坐标轴的比例尺,分别作出各典型环节频率特性的Bode图,即分别在对数幅频特性图和对数相频特性图中作出对数幅频特性的渐近线和对数相频特性曲线;如图所示:
5)对各环节的对数幅频特性图和对数相频特性图进行叠加。首先将无转折频率的环节(放大、积分或微分)叠加。然后以转折频率为分界点,分段进行叠加,其实质是曲线的斜率相加。
利用上述方法得到如图所示的幅频曲线(用红粗实线示出)。
绘制开环系统对数频率特性曲线的一般步骤
1)将系统的传递函数转化为若干个典型环节的传递函数(标准形式,即典型环节传递函数中的常数项化成1)相乘的形式;
2)确定系统的开环频率特性,并保留各环节相乘的形式;
3)确定典型环节的特征参数(如:比例系数、转折频率、无阻尼固有频率等),以便确定它们的渐近线; 自动控制网www.eadianqi.com版权所有
4)选定坐标轴的比例尺,分别作出各典型环节频率特性的Bode图,即分别在对数幅频特性图和对数相频特性图中作出对数幅频特性的渐近线和对数相频特性曲线;
5)对各环节的对数幅频特性图和对数相频特性图进行叠加。首先将无转折频率的环节(放大、积分或微分)叠加。然后以转折频率为分界点,分段进行叠加,其实质是曲线的斜率相加。
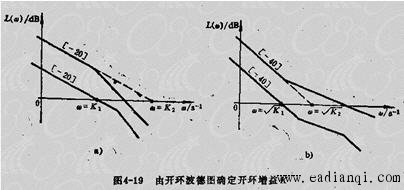
确定开环增益K的大小还可以通过图4-19所示的方法。下图a所示为v=1的情况下,起始段斜率为[-20],起始段(或其延长线)与0dB线相交处的频率等于K值, 自动控制网www.eadianqi.com版权所有
 自动控制网www.eadianqi.com版权所有
因为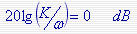 故有K等于交点处的频率值。 故有K等于交点处的频率值。
对于II型系统,如图b所示,起始段斜率为[-40],其与0dB线交点处的频率等于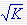 值,因为 值,因为 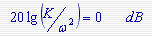
与上述作图过程相反,在已知开环Bode图时,应能写出开环传递函数。
最小相位系统
在传递函数G(s)的所有零点和极点均在复平面[s]的左半平面内,则称G(s)为最小传递函数,具有最小相位传递函数的系统称为最小相位系统;
反之,若传递函数G(s) 在复平面[s]的右半平面内存在零点或极点,则称G(s)为非最小传递函数,具有非最小相位传递函数的系统称为非最小相位系统。
具有相同幅频特性的系统,最小相位系统的相角变化范围是最小的。
例如两个系统的传递函数分别为 本文来自www.eadianqi.com

两个系统的零、极点分布图为 本文来自www.eadianqi.com
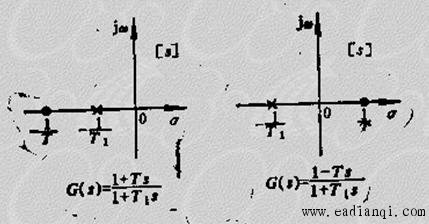
显然,G1(s)属于最小相位系统。其Bode图如下
从图中可以看出:两个系统的幅值相同,具有同一个幅频特性,但却有不同的相频特性。非最小相位系统在高频时的相角滞后大,启动性能不佳,响应缓慢,因此,在要求响应比较快的系统中,就不能选用非最小相位元件。 本文来自www.eadianqi.com
|

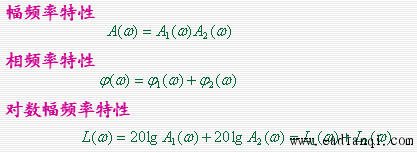

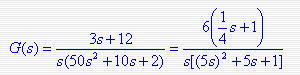 上式将系统的传递函数化为比例、积分、振荡、一阶微分四个环节组成。
上式将系统的传递函数化为比例、积分、振荡、一阶微分四个环节组成。