1. 系统的误差与偏差
1)系统的误差 e(t)
误差信号e(t)为系统的希望输出与系统的实际输出x0(t)之差,即 e(t)= x0r(t) - x0(t)其拉氏变换E(s)= X0r(s) - X0(s)
2)稳态误差 ess
系统达到稳定状态后,系统的实际输出量与系统希望的输出量之间的偏差称为稳态误差。也是系统误差e(t)的瞬态分量消失后的稳态误差(即系统误差e(t)的稳态分量)。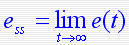
3)系统的偏差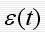
控制系统的输入信号与反馈信号之间的差值称为系统的偏差。  其拉氏变换 其拉氏变换
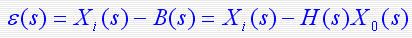
4)偏差与误差间的关系
 本文来自www.eadianqi.com
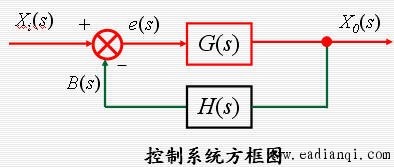
一个闭环控制系统之所以能对输出 X0(s)起自动控制作用,在于运用偏差e(s)进行控制,即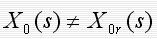 时有 时有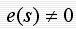 ,就通过e(s)进行控制,企图将X0(s)调节到X0r(s);反之,当X0(s)= X0r(s)时,而e(s)=0, e(s)不再对X0(s)进行调节,此时,控制系统无控制作用。 ,就通过e(s)进行控制,企图将X0(s)调节到X0r(s);反之,当X0(s)= X0r(s)时,而e(s)=0, e(s)不再对X0(s)进行调节,此时,控制系统无控制作用。

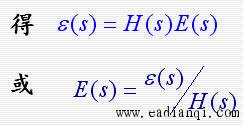
由上式可知:在求得偏差 10 后即可求出误差,对于单位反馈系统,H(s)=1;此时,误差与偏差相同。
2 稳态误差的计算
一般情况下,求系统的稳态误差ess,必须首先求出系统的误差e(t),然后计算当 时的极限,为了简化计算,可应用拉氏变换的终值定理计算误差,即 时的极限,为了简化计算,可应用拉氏变换的终值定理计算误差,即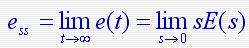 条件:当sE(s)的全部极点都分布在[s]平面的左半平面(包括坐标原点),即系统处于稳定状态。当系统的传递函数确定后,由输入信号引起的误差与输入信号之间的关系可以确定,由式E(s)= X0r(s) - X0(s) 自动控制网www.eadianqi.com版权所有 条件:当sE(s)的全部极点都分布在[s]平面的左半平面(包括坐标原点),即系统处于稳定状态。当系统的传递函数确定后,由输入信号引起的误差与输入信号之间的关系可以确定,由式E(s)= X0r(s) - X0(s) 自动控制网www.eadianqi.com版权所有
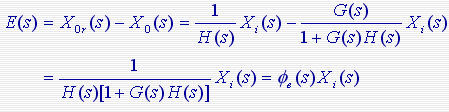 式中 式中 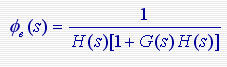 称为误差传递函数则 称为误差传递函数则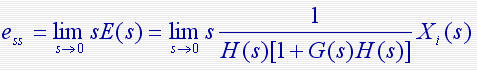 式中H(s)、G(s)分别为系统的反馈传递函数和前向传递函数,G(s)H(s)为系统的开环传递函数。可以用上式计算不同输入信号X(s)产生的稳态误差。 式中H(s)、G(s)分别为系统的反馈传递函数和前向传递函数,G(s)H(s)为系统的开环传递函数。可以用上式计算不同输入信号X(s)产生的稳态误差。
例题
已知单位反馈系统的开环传递函数为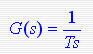 求其在单位阶跃输入、单位速度输入、单位加速度输入以及正弦信号 求其在单位阶跃输入、单位速度输入、单位加速度输入以及正弦信号 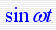 输入下的稳态误差。 输入下的稳态误差。
解:该单位反馈系统在输入作用下的误差传递函数为: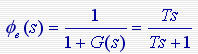
单位阶跃输入: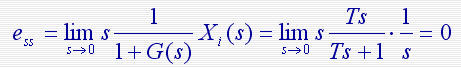 自动控制网www.eadianqi.com版权所有
单位速度输入: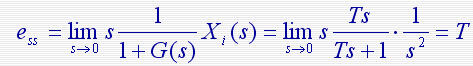
单位加速度输入: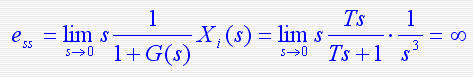
对于 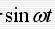 输入:则误差信号e(t)的拉氏变换 输入:则误差信号e(t)的拉氏变换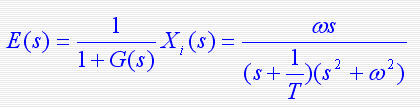 由于上式在虚轴上有一对共轭极点,不能用拉氏变换的终值定理来求稳态误差。 由于上式在虚轴上有一对共轭极点,不能用拉氏变换的终值定理来求稳态误差。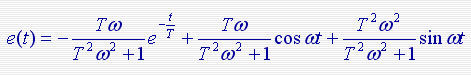
则稳态误差:
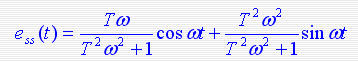
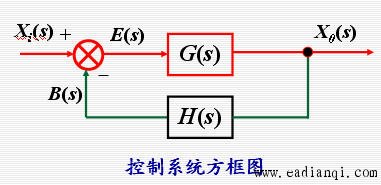
2. 与输入和系统结构有关的稳态误差
分析如下图所示的系统的稳态误差ess 本文来自www.eadianqi.com
因为
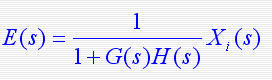
由终值定理得系统的稳态误差为
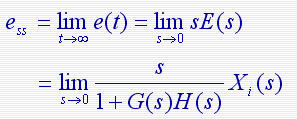
很显然,系统的稳态误差不仅与系统的结构、参数有关,而且与系统的输入特性有关。为了简化稳态误差的计算,定义:

则 1)当系统的输入为单位阶跃信号 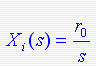 时,系统的稳态误差为 时,系统的稳态误差为 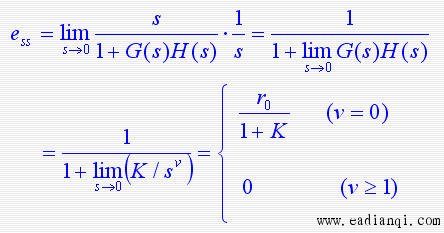
因此,在阶跃输入下,系统消除误差的条件是v>=1,即在开环传递函数中至少有一个积分环节。 本文来自www.eadianqi.com
2)当系统的输入为单位斜坡信号 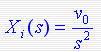 时,系统的稳态误差为 时,系统的稳态误差为
因此,在斜坡输入下,系统消除误差的条件是v>=2。即在开环传递函数中至少有两个积分环节。
3)当系统的输入为单位加速度信号 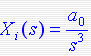 时,系统的稳态误差为 时,系统的稳态误差为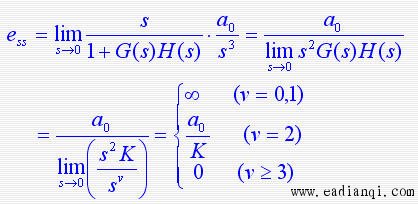
因此,在单位加速度输入下,系统消除误差的条件是v>=3,即在开环传递函数中至少有三个积分环节。
设系统的开环传递函数为
式中K为开环增益,v为开环传递函数中包含积分环节的数目。
根据v来区分系统的型次,当v分别为0,1,2,…时,分别称系统为0型系统、I型系统、 II型系统等等。 本文来自www.eadianqi.com



显然,位置无偏系数Kp,速度无偏系数Kv 和加速度无偏系数Ka 与系统的型次v和开环增益K有关。系统开环的型次与误差系数以及输入信号形式和系统稳态误差之间的关系见下表:
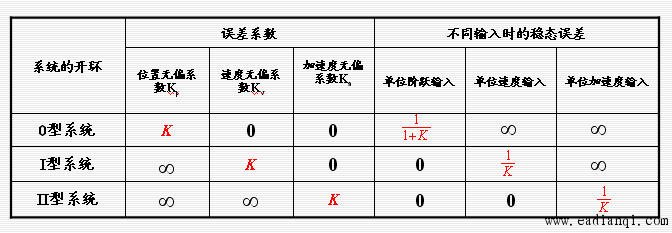
从上表可以看出:同一系统在不同的输入作用下,其稳态误差是不同的。特别有意义的是:对于同一种输入,当系统的型次增加时,系统的准确性将得到提高;增加系统的开环增益,往往也可以提高系统的稳态精度。但是,系统的型次和开环增益的增加,却使得系统的稳定性变差。因此,通常需要在系统的稳定性和准确性之间进行权衡,必要时,需要引入校正环节进行校正。
例题
控制系统(比例加微分)的方框图如图所示,若输入信号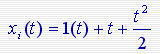 ,试求系统的稳态误差 ,试求系统的稳态误差 本文来自www.eadianqi.com 本文来自www.eadianqi.com
解:该系统含有两个积分环节,是一个II型系统。其开环增益为K1Km,因此
当输入xi(t)=1(t)时, ess1=0
当输入xi(t)=t 时, ess2=0
当输入xi(t)=t^2/2时, ess3=1/K=1/K1Km
所以系统的稳态误差为 ess = ess1 + ess2 + ess3 =1/K1Km
几点说明:
1)系统必须是稳定的;
2)K是系统开环增益;
3)表3-2显示的规律是在单位反馈情况下建立的;
4)上述结论不适应干扰输入作用下的误差。 本文来自www.eadianqi.com
|
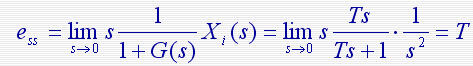
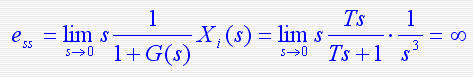
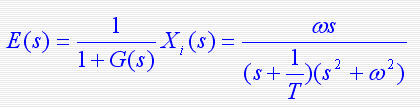 由于上式在虚轴上有一对共轭极点,不能用拉氏变换的终值定理来求稳态误差。
由于上式在虚轴上有一对共轭极点,不能用拉氏变换的终值定理来求稳态误差。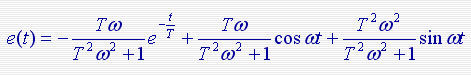
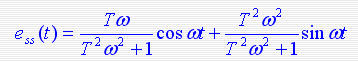


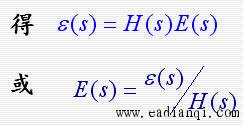
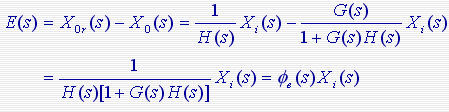 式中
式中 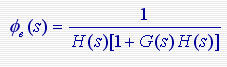 称为误差传递函数则
称为误差传递函数则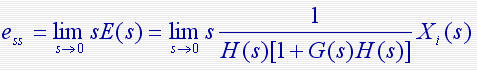 式中H(s)、G(s)分别为系统的反馈传递函数和前向传递函数,G(s)H(s)为系统的开环传递函数。可以用上式计算不同输入信号X(s)产生的稳态误差。
式中H(s)、G(s)分别为系统的反馈传递函数和前向传递函数,G(s)H(s)为系统的开环传递函数。可以用上式计算不同输入信号X(s)产生的稳态误差。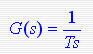 求其在单位阶跃输入、单位速度输入、单位加速度输入以及正弦信号
求其在单位阶跃输入、单位速度输入、单位加速度输入以及正弦信号 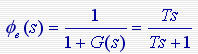
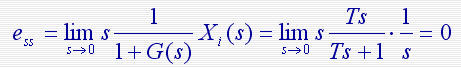

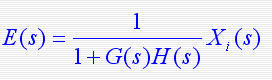
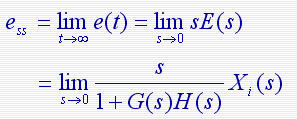

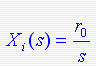 时,系统的稳态误差为
时,系统的稳态误差为 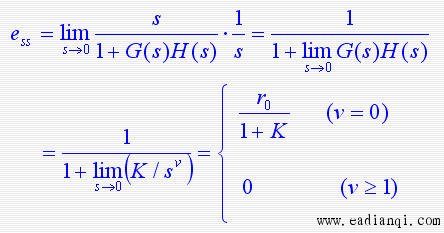
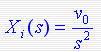 时,系统的稳态误差为
时,系统的稳态误差为
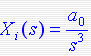 时,系统的稳态误差为
时,系统的稳态误差为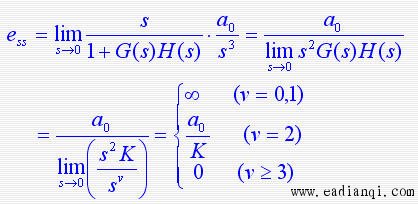





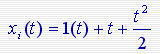 ,试求系统的稳态误差
,试求系统的稳态误差