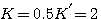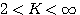|
得 本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有 实部方程 本文来自www.eadianqi.com
虚部方程 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有
解得 自动控制网www.eadianqi.com版权所有
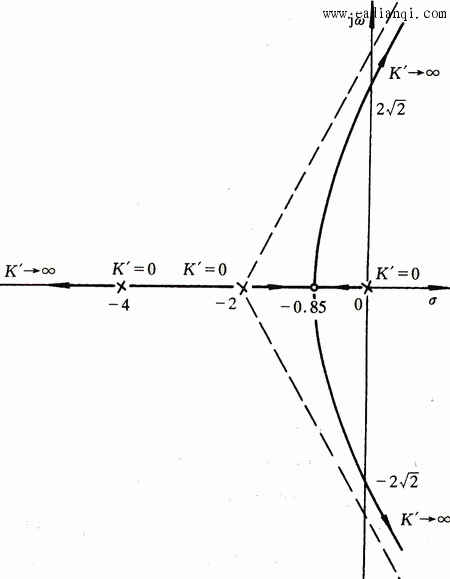
本文来自www.eadianqi.com 图3.29是该系统的根轨迹图。 自动控制网www.eadianqi.com版权所有
图3.29 例17的根轨迹 本文来自www.eadianqi.com
例18 控制系统的开环传递函数为: 本文来自www.eadianqi.com
本文来自www.eadianqi.com
试绘制系统的根轨迹。 本文来自www.eadianqi.com
本文来自www.eadianqi.com
(4)根轨迹在实轴上的部分是0到-2,-3到负无穷大。 自动控制网www.eadianqi.com版权所有
将图3.30各角的值代入式(3.155), 自动控制网www.eadianqi.com版权所有
根据根轨迹的对称性,复数开环极点-1-j的出射角为
(7)与虚轴交点,将S=j 自动控制网www.eadianqi.com版权所有
代入S=j 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有
虚部方程 本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有 解此方程组,得 本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有
图3.31是系统的根轨迹图。 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
3.9.4 根轨迹法分析系统性能
分析该系统的稳定性并利用根轨迹法校正系统的稳定性。 本文来自www.eadianqi.com
求使系统稳定的范围。 本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有
式中K称为开环放大系统,
二者相差一个比例常数,比例常数是由时间常数和零极点的数值决定的。 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有
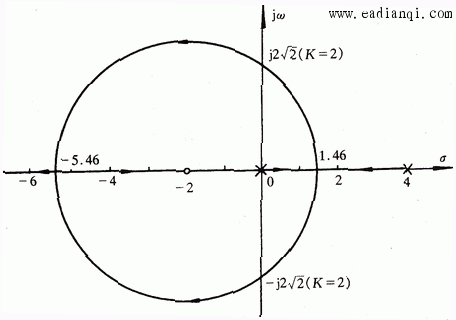
系统根轨迹如图3.34所示。
自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
由
所以,当开环放大系数K的范围为 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有
系统是稳定的。 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
|
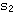 不在根轨迹上,不是分离点。分离点为s=-0.85。
不在根轨迹上,不是分离点。分离点为s=-0.85。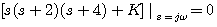
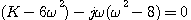
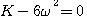 本文来自www.eadianqi.com
本文来自www.eadianqi.com 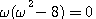
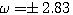 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 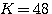
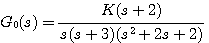
 j1。
j1。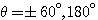
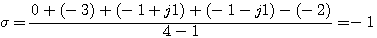
 j为共轭复数极点。开环零点分布入图3.30所示。
j为共轭复数极点。开环零点分布入图3.30所示。 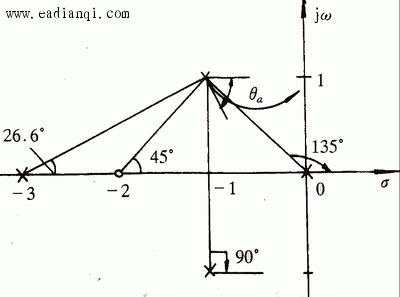
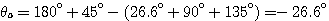 本文来自www.eadianqi.com
本文来自www.eadianqi.com 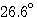 。 自动控制网www.eadianqi.com版权所有
。 自动控制网www.eadianqi.com版权所有 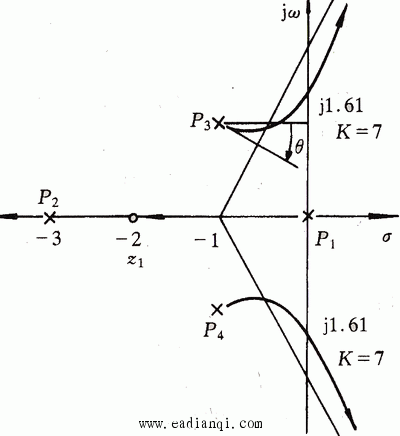
 代入特征方程。特征方程为
代入特征方程。特征方程为 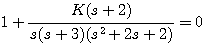 本文来自www.eadianqi.com
本文来自www.eadianqi.com 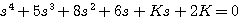
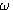 并整理后得
并整理后得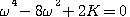
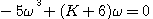
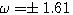
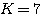


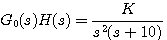
 型系统,对单位阶跃和单位斜坡输入函数响应的稳态误差为零。系统的单位阶跃响应,是衰减振荡过程。
型系统,对单位阶跃和单位斜坡输入函数响应的稳态误差为零。系统的单位阶跃响应,是衰减振荡过程。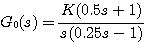 本文来自www.eadianqi.com
本文来自www.eadianqi.com 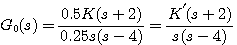
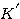 称为根轨迹放大系数
称为根轨迹放大系数 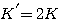

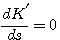 本文来自www.eadianqi.com
本文来自www.eadianqi.com 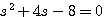
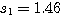
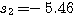
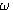 代入特征方程,可求得 本文来自www.eadianqi.com
代入特征方程,可求得 本文来自www.eadianqi.com 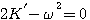
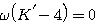
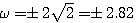
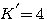
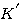 可计算出系统的开环放大系数
可计算出系统的开环放大系数