|
在控制系统的时域分析中,求取高阶系统的响应时间是一件十分困难的工作。而利用计算机,则可以方便地求出系统在一系列时刻上瞬态响应的数值解,并且可以满足精度上的要求。这就是控制系统的数值分析法。
不论高阶微分方程或是状态空间表达式,都有微分方程的求解问题。对n阶微分方程求解,必须进行n次积分运算。所以,数值积分法就成为控制系统数值分析的最基本算法。
设一阶微分方程为 本文来自www.eadianqi.com
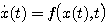 本文来自www.eadianqi.com
初始条件为 自动控制网www.eadianqi.com版权所有
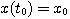 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
把方程改写为 自动控制网www.eadianqi.com版权所有
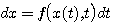 (3.125) 本文来自www.eadianqi.com (3.125) 本文来自www.eadianqi.com
如果我们把积分区间划分为若干子区间: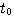 , ,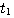 , ,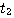 , , ,对方程(3.125)两边从 ,对方程(3.125)两边从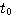 到 到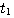 积分 积分 本文来自www.eadianqi.com
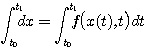 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
可以得到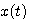 在 在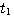 时刻的值 自动控制网www.eadianqi.com版权所有 时刻的值 自动控制网www.eadianqi.com版权所有
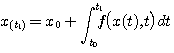 (3.126) (3.126) 本文来自www.eadianqi.com
求出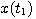 后,则可以根据 后,则可以根据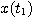 再求出 再求出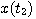 的值 自动控制网www.eadianqi.com版权所有 的值 自动控制网www.eadianqi.com版权所有
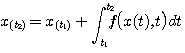 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
按同样的方法依次递推,就可以一步一步计算出整个积分区间内一系列时刻的方程的数值解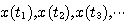 。 。
在上述计算中,积分区间时间段的划分一般是均匀划分,我们称相邻两个时刻的时间间隔为计算步长,用h表示,则有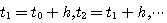 。 。
实际上式(3.126)那样的递推公式是不能计算出结果,因为方程右边含有未知函数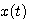 。从微分方程 本文来自www.eadianqi.com 。从微分方程 本文来自www.eadianqi.com
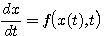 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
知道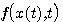 是 是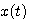 在t时刻的切线斜率。要使式(3.126)能够计算,必须设法确定 在t时刻的切线斜率。要使式(3.126)能够计算,必须设法确定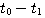 时刻段上 时刻段上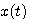 的斜率 的斜率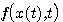 。在计算步长取得足够小时,我们可以认为 。在计算步长取得足够小时,我们可以认为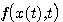 在 在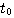 到 到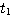 区间是一个常数。怎样寻求这个常数值f,有多种方法。最简单的一种方法是认为 区间是一个常数。怎样寻求这个常数值f,有多种方法。最简单的一种方法是认为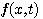 在 在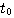 到 到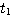 区间的斜率等于函数在 区间的斜率等于函数在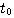 时刻的斜率,即 时刻的斜率,即 自动控制网www.eadianqi.com版权所有
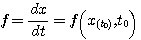 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
则(3.126)式因而可以写成 本文来自www.eadianqi.com
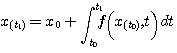 (3.127) (3.127) 自动控制网www.eadianqi.com版权所有
因为f在 到 到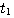 区间内是常量,所以式(3.127)就变为 区间内是常量,所以式(3.127)就变为 自动控制网www.eadianqi.com版权所有
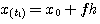 (3.128) 本文来自www.eadianqi.com (3.128) 本文来自www.eadianqi.com
推广到一般表达式 本文来自www.eadianqi.com
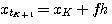 (3.129) 本文来自www.eadianqi.com (3.129) 本文来自www.eadianqi.com
式中 本文来自www.eadianqi.com
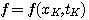 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
这就是最简单的数值积分方法——欧拉法。
欧拉法由于算法简单,误差较大,实际计算中很少使用。
工程上应用较普遍的一种数值积分法是四阶龙格-库塔(Rungekutta)法。四阶龙格-库塔法的计算公式为 自动控制网www.eadianqi.com版权所有
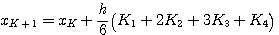 (3.130) (3.130) 自动控制网www.eadianqi.com版权所有
式中 本文来自www.eadianqi.com
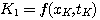 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
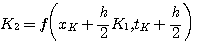 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
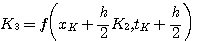 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
 本文来自www.eadianqi.com 本文来自www.eadianqi.com
四阶龙格-库塔法在计算常量f时,不像欧拉法那样只取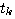 时刻的斜率代替整个 时刻的斜率代替整个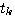 到 到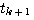 区间的斜率,而是以不同方法计算出4个斜率值 区间的斜率,而是以不同方法计算出4个斜率值 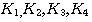 并进行加权平均。这样的道德平均斜率更接近于原来的曲线,因而精度较高。 并进行加权平均。这样的道德平均斜率更接近于原来的曲线,因而精度较高。
当系统的数学模型是微分方程或传递函数时,一般先要变换成状态空间表达式。因为上述数值积分法是一阶微分方程的积分法,而状态方程的各方成都是一阶微分方程,只需对每一个方程进行重复平行的计算就可以了。 自动控制网www.eadianqi.com版权所有
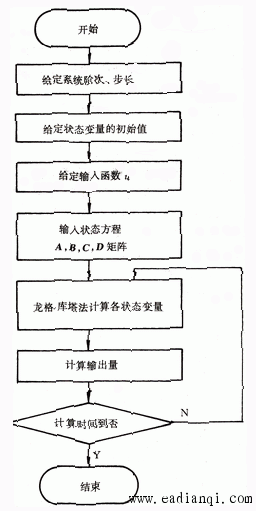
图3.25 状态方程数值积分程序框图 自动控制网www.eadianqi.com版权所有
图3.25是状态方程求数值解的一个程序流程图。
数值积分的实用程序在很多书中都有介绍,针对控制系统数值分析还专门开发了许多软件,用户可以很方便的根据状态方程或系统结果图进行编程分析。
在控制系统的数值分析中,计算步长的选择很重要。步长选得过大,计算精度较低。步长选得过小,计算量大。应用四阶龙格-库塔法,根据经验,可选 自动控制网www.eadianqi.com版权所有
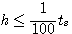 本文来自www.eadianqi.com 本文来自www.eadianqi.com
式中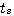 是控制系统的调节时间。 是控制系统的调节时间。
数值分析只能得到控制系统离散的数值响应,不可能得到解析解,这不利于研究系统的内在规律。
控制系统的动态特性,稳态特性性能指标,可以按定义从数值解中求出。
控制系统的数值分析方法又称为控制系统的数字仿真。在控制系统的分析与设计中,数字仿真技术应用十分普遍,已成为时域分析法中一种重要的方法。 自动控制网www.eadianqi.com版权所有
|
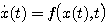
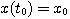
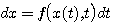 (3.125)
(3.125) 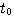 ,
,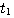 ,
,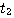 ,
, ,对方程(3.125)两边从
,对方程(3.125)两边从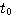 到
到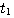 积分
积分 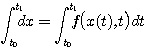 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 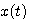 在
在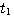 时刻的值
时刻的值 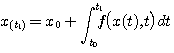 (3.126)
(3.126) 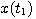 后,则可以根据
后,则可以根据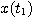 再求出
再求出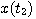 的值 自动控制网www.eadianqi.com版权所有
的值 自动控制网www.eadianqi.com版权所有 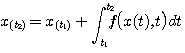
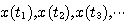 。
。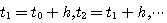 。
。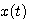 。从微分方程
。从微分方程 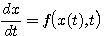
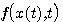 是
是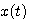 在t时刻的切线斜率。要使式(3.126)能够计算,必须设法确定
在t时刻的切线斜率。要使式(3.126)能够计算,必须设法确定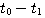 时刻段上
时刻段上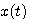 的斜率
的斜率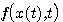 。在计算步长取得足够小时,我们可以认为
。在计算步长取得足够小时,我们可以认为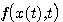 在
在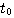 到
到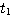 区间是一个常数。怎样寻求这个常数值f,有多种方法。最简单的一种方法是认为
区间是一个常数。怎样寻求这个常数值f,有多种方法。最简单的一种方法是认为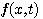 在
在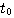 到
到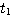 区间的斜率等于函数在
区间的斜率等于函数在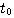 时刻的斜率,即
时刻的斜率,即 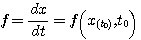 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 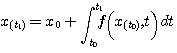 (3.127)
(3.127)  到
到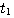 区间内是常量,所以式(3.127)就变为
区间内是常量,所以式(3.127)就变为 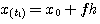 (3.128)
(3.128) 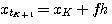 (3.129)
(3.129) 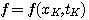 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 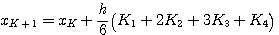 (3.130)
(3.130) 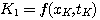
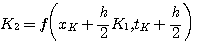
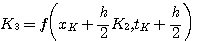 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有  本文来自www.eadianqi.com
本文来自www.eadianqi.com 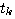 时刻的斜率代替整个
时刻的斜率代替整个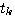 到
到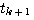 区间的斜率,而是以不同方法计算出4个斜率值
区间的斜率,而是以不同方法计算出4个斜率值 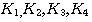 并进行加权平均。这样的道德平均斜率更接近于原来的曲线,因而精度较高。
并进行加权平均。这样的道德平均斜率更接近于原来的曲线,因而精度较高。
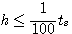 本文来自www.eadianqi.com
本文来自www.eadianqi.com 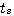 是控制系统的调节时间。
是控制系统的调节时间。