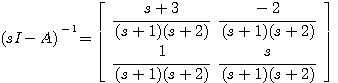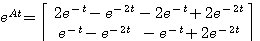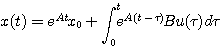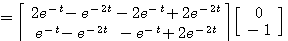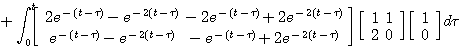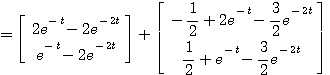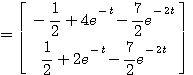|
以上讨论的控制系统的分析方法,都是基于控制系统的数学模型是传递函数或输入——输出微分方程。在时域分析中,若控制系统的数学模型是状态空间表达式,我们就必须考虑状态方程的求解问题。 自动控制网www.eadianqi.com版权所有
3.6.1 线性定常系统状态方程的解
状态方程的求解,就是在给定的初始值x(0)条件下,确定系统在输入u(t)的作用下在t时刻的状态响应x(t)。 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 式中a,b为常数,方程的初始条件为 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com 对式(3.108)两边去拉普拉斯变换 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
整理后得 自动控制网www.eadianqi.com版权所有
对上式两边进行拉普拉斯反变换得 本文来自www.eadianqi.com
本文来自www.eadianqi.com
其中,指数函数
本文来自www.eadianqi.com
状态方程是由n个一阶微分方程组成的,其解法也与一阶微分方程的解法及其类似。 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有
初始条件为 自动控制网www.eadianqi.com版权所有
对式(3.111)两边取拉普拉斯变换得 本文来自www.eadianqi.com
本文来自www.eadianqi.com
进而得 自动控制网www.eadianqi.com版权所有
对(3.112)式两边求拉普拉斯的变换得 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
本文来自www.eadianqi.com
式中, 本文来自www.eadianqi.com
矩阵指数具有如下性质 本文来自www.eadianqi.com
本文来自www.eadianqi.com
齐次状态方程的解还可以写成 自动控制网www.eadianqi.com版权所有
式中 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 状态转移矩阵具有如下性质 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
本文来自www.eadianqi.com
本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有
对于非齐次状态方程 自动控制网www.eadianqi.com版权所有
可以写成 本文来自www.eadianqi.com
本文来自www.eadianqi.com
两边左乘 自动控制网www.eadianqi.com版权所有
即 自动控制网www.eadianqi.com版权所有
对上式积分 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有
两边再左乘 本文来自www.eadianqi.com
(3.121)式也可以用状态转移矩阵表示 本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有
式中 自动控制网www.eadianqi.com版权所有
非齐次状态方程的解可以分为两部分,第一项表示了系统自由运动的特性,是初始状态转移项,叫零输入响应。后一项表示了系统受迫运动的特性,起因于输入向量,叫做零状态响应。 自动控制网www.eadianqi.com版权所有
3.6.2 状态转移矩阵的计算
自动控制网www.eadianqi.com版权所有
例7 线性定常系统的状态方程为 本文来自www.eadianqi.com
本文来自www.eadianqi.com
计算其状态转移矩阵。 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
用拉普拉斯变换法计算状态转移矩阵,进行矩阵的求逆运算和求拉普拉斯反变换,在系统阶数较高时,计算非常烦杂。 自动控制网www.eadianqi.com版权所有
例8 已知线性定常系统状态方程的系统矩阵A为 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
计算其状态转移矩阵。
直接计算法得到的状态转移矩阵,矩阵中每个元素都是一个无穷级数,其缺点是系统阶数较高时,计算量很大,另外,无穷级数不容易写成闭式解析表达式。
自动控制网www.eadianqi.com版权所有 设初始值为 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
输入向量为 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有
求此状态方程的解。
所以 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
本文来自www.eadianqi.com
本文来自www.eadianqi.com
|
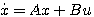 (3.107)
(3.107) 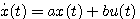 (3.108)
(3.108) 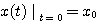
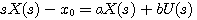
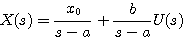
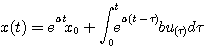 (3.109)
(3.109) 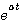 可以展开成无穷级数 本文来自www.eadianqi.com
可以展开成无穷级数 本文来自www.eadianqi.com 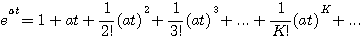
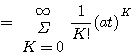 (3.110)
(3.110) 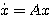 (3.111)
(3.111) 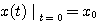 本文来自www.eadianqi.com
本文来自www.eadianqi.com 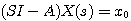
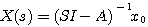 (3.112)
(3.112) 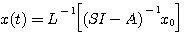

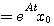 (3.113)
(3.113)  称为矩阵指数,A为n*n维方阵,
称为矩阵指数,A为n*n维方阵,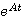 也是一个无穷级数
也是一个无穷级数 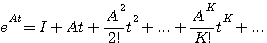
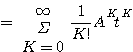 (3.114)
(3.114) 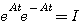 (3.115) 本文来自www.eadianqi.com
(3.115) 本文来自www.eadianqi.com 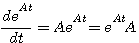 (3.116) 自动控制网www.eadianqi.com版权所有
(3.116) 自动控制网www.eadianqi.com版权所有  (3.117)
(3.117) 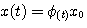 (3.118)
(3.118) 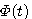 称为状态转移矩阵,是n*n维矩阵。式(3.118)说明,状态方程(3.111)的解就是状态从初始状态向t时刻状态的转移,所以把
称为状态转移矩阵,是n*n维矩阵。式(3.118)说明,状态方程(3.111)的解就是状态从初始状态向t时刻状态的转移,所以把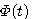 称为状态转移矩阵。显然,对线性定常系统
称为状态转移矩阵。显然,对线性定常系统 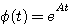 (3.119)
(3.119) 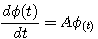
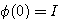 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 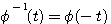
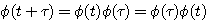
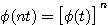
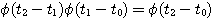
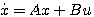 (3.120) 自动控制网www.eadianqi.com版权所有
(3.120) 自动控制网www.eadianqi.com版权所有 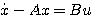
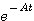
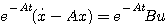 本文来自www.eadianqi.com
本文来自www.eadianqi.com  自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 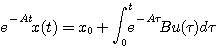
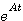 得
得 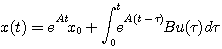 (3.121) 自动控制网www.eadianqi.com版权所有
(3.121) 自动控制网www.eadianqi.com版权所有 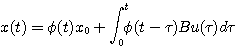 (3.122)
(3.122) 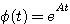
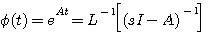 (3.123)
(3.123) 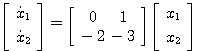
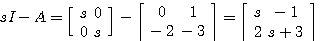
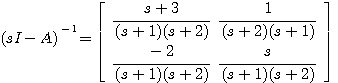
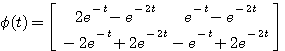
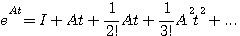
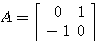
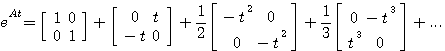
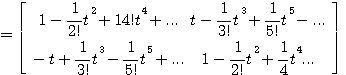
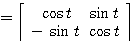 本文来自www.eadianqi.com
本文来自www.eadianqi.com 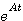 化为对角线矩阵等,在这里不再叙述。有必要时请参看其他书籍。
化为对角线矩阵等,在这里不再叙述。有必要时请参看其他书籍。

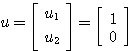
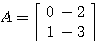
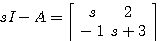 本文来自www.eadianqi.com
本文来自www.eadianqi.com