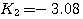|
根轨迹法是控制系统的一种实用分析方法。
3.9.1 根轨迹的概念
控制系统的稳定性、动态特性都与特征方程的根(即闭环极点)在s平面上的分布有密切关系。时域分析中,依靠求解输入——输出微分方程或状态方程,只能确定控制系统闭环极点的具体分布。若要研究参数变化对控制系统性能的影响,特别是某些参数连续变化对系统性能的影响,依靠求解特征方程的方法来确定闭环极点的位置随参数变化的情况,计算量很大,有时甚至是不可能的。现在,我们则可以通过一种简便的图解方法,很方便地给出特征方程的根随参数变化在s平面上分布位置变化的情况。我们先看下面的例子。
例16 设单位反馈系统的开环传递函数为: 自动控制网www.eadianqi.com版权所有
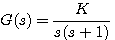 本文来自www.eadianqi.com 本文来自www.eadianqi.com
当开环放大系数K从零到无穷大变化时,系统的特征根在s平面上怎样分布?
解 系统有两个开环极点 本文来自www.eadianqi.com
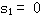 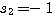 本文来自www.eadianqi.com
系统的闭环传递函数为 自动控制网www.eadianqi.com版权所有
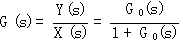 自动控制网www.eadianqi.com版权所有
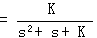 本文来自www.eadianqi.com 本文来自www.eadianqi.com
系统的特征方程为 自动控制网www.eadianqi.com版权所有
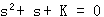 本文来自www.eadianqi.com
特征方程的根 自动控制网www.eadianqi.com版权所有
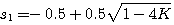 本文来自www.eadianqi.com 本文来自www.eadianqi.com
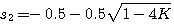 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
可见特征根在s平面的位置与K有关。
K=0时,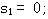 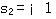 ,与开环极点的位置相同。 ,与开环极点的位置相同。
0<K<1/4时,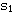 , ,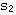 均为负实数,分布在0到-1之间,随K从零开始逐渐增大, 均为负实数,分布在0到-1之间,随K从零开始逐渐增大,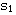 和 和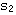 也从开环极点的位置开始逐渐接近。 也从开环极点的位置开始逐渐接近。
K=1/4时,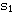 = =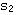 =-0.5,两个闭环极点重合。 =-0.5,两个闭环极点重合。 本文来自www.eadianqi.com
K>1/4时,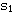 和 和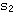 都成为共轭复数。 本文来自www.eadianqi.com 都成为共轭复数。 本文来自www.eadianqi.com
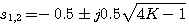 本文来自www.eadianqi.com
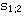 具有相同的负实部,且为常数,而虚部则随K的增加其绝对值也增加。图3.28给出了系统的特征根在K从零变化到无穷大时,相应位置的变化情况。 具有相同的负实部,且为常数,而虚部则随K的增加其绝对值也增加。图3.28给出了系统的特征根在K从零变化到无穷大时,相应位置的变化情况。
这种放大系数K从零到无穷大变化时,特征方程的根在s平面上相应变化的轨迹,称为根轨迹。根轨迹完整地反映了特征根随参数变化的情况。根据图3.28的根轨迹图,我们可以知道,在K<1/4时,系统的单位阶跃响应中含有两个指数项函数。在K=1/4时,两个指数项函数合二为一。在K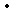 1/4时,根轨迹进入复平面,说明系统的单位阶跃响应由单调变化转变为振荡。从图还可以看出,不论K怎样变化,系统始终是稳定的。因为全部根轨迹都分布在s平面左半边。 1/4时,根轨迹进入复平面,说明系统的单位阶跃响应由单调变化转变为振荡。从图还可以看出,不论K怎样变化,系统始终是稳定的。因为全部根轨迹都分布在s平面左半边。 本文来自www.eadianqi.com
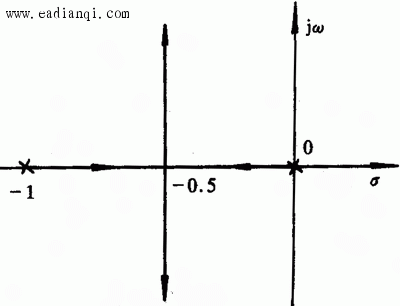
图3.28 特征根随K的变化情况 自动控制网www.eadianqi.com版权所有
3.9.2 根轨迹的基本条件
控制系统的特征方程为 本文来自www.eadianqi.com
 (3.145) 本文来自www.eadianqi.com (3.145) 本文来自www.eadianqi.com
式中 为系统前向通道传递函数,H(s)为系统反馈通道传递函数。上式可改写为 为系统前向通道传递函数,H(s)为系统反馈通道传递函数。上式可改写为 本文来自www.eadianqi.com
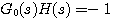 (3.146) (3.146) 本文来自www.eadianqi.com
将系统的开环传递函数写成零极点形式 本文来自www.eadianqi.com
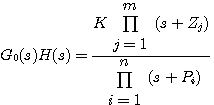 (3.147) 本文来自www.eadianqi.com (3.147) 本文来自www.eadianqi.com
式中K称为根轨迹放大系数或根轨迹增益。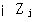 称为开环零点, 称为开环零点,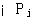 称为开环极点。 称为开环极点。
将(3.147)式代入(3.146)式得 自动控制网www.eadianqi.com版权所有
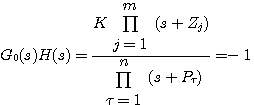 (3.148) (3.148) 自动控制网www.eadianqi.com版权所有
式(3.148)是一个复数方程,可以用复数的幅值和幅角分别表示为 本文来自www.eadianqi.com
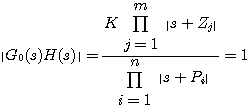 (3.149) (3.149) 本文来自www.eadianqi.com
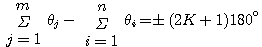 , , 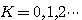 (3.150) (3.150) 自动控制网www.eadianqi.com版权所有
式中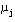 是矢量 是矢量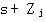 与实轴正方向的夹角, 与实轴正方向的夹角,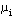 是矢量 是矢量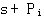 与实轴正方向的夹角。我们称式(3.149)为根轨迹的幅值条件,式(3.150)为根轨迹的幅角条件。凡在根轨迹上的点都是系统特征方程的根,都必须同时满足根轨迹的幅值条件和幅角条件。这两个条件统称为根轨迹的基本条件。 本文来自www.eadianqi.com 与实轴正方向的夹角。我们称式(3.149)为根轨迹的幅值条件,式(3.150)为根轨迹的幅角条件。凡在根轨迹上的点都是系统特征方程的根,都必须同时满足根轨迹的幅值条件和幅角条件。这两个条件统称为根轨迹的基本条件。 本文来自www.eadianqi.com
3.9.3 根轨迹的绘制规则
根轨迹法是分析控制系统的一种图解方法,正确地绘制出根轨迹图是进行根轨迹分析的基础。根轨迹图的绘制,并不要求求解特征方程,而是根据根轨迹的基本条件,导出一些简单实用的法则,画出根轨迹图形。
绘制根轨迹的规则有:
1.根轨迹的分支
n阶系统的特征方程是关于s的n次代数方程,方程有n个解,所以系统的根轨迹有n条。也就是说,根轨迹有n条分支。
2.根轨迹的起点与终点
将式(3.148)写成 自动控制网www.eadianqi.com版权所有
 (3.151) 自动控制网www.eadianqi.com版权所有 (3.151) 自动控制网www.eadianqi.com版权所有
当K=0时,上式右边为无穷大,左边只有当s趋于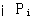 时才会是无穷大。根轨迹的起点是K=0时的根轨迹,所以说根轨迹起始于开环极点。 时才会是无穷大。根轨迹的起点是K=0时的根轨迹,所以说根轨迹起始于开环极点。
K趋于无穷大时的根轨迹,称为根轨迹的终点。从式(3.151)可以看出,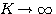 时,方程右边为零,而方程左边只有在 时,方程右边为零,而方程左边只有在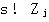 时才会为零。所以可以说根轨迹终止于开环零点。控制系统中,若n>m,m条根轨迹终止于开环零点,还有(n-m)条根轨迹则终止于无穷远处。这时因为,当 时才会为零。所以可以说根轨迹终止于开环零点。控制系统中,若n>m,m条根轨迹终止于开环零点,还有(n-m)条根轨迹则终止于无穷远处。这时因为,当 时,由于n>m,同样有 本文来自www.eadianqi.com 时,由于n>m,同样有 本文来自www.eadianqi.com
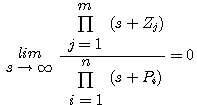 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
3.根轨迹的渐近线
终止于无穷远处的(n-m)条根轨迹,在 时,沿渐近线变化。渐近线确定了终止于无穷远处的根轨迹的变化方向。 时,沿渐近线变化。渐近线确定了终止于无穷远处的根轨迹的变化方向。
渐近线与实轴正方向的夹角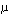 为 为 本文来自www.eadianqi.com
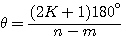 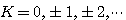 (3.152) 本文来自www.eadianqi.com (3.152) 本文来自www.eadianqi.com
渐近线与实轴的交点为 自动控制网www.eadianqi.com版权所有
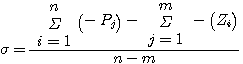 (3.153) (3.153) 本文来自www.eadianqi.com
式(3.153)可以表述为 本文来自www.eadianqi.com
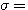 (所有开环极点之和-所有开环零点之和)/n-m 本文来自www.eadianqi.com (所有开环极点之和-所有开环零点之和)/n-m 本文来自www.eadianqi.com
4.根轨迹的对称性
特征方程的根不是实数就是共轭复数,所以根轨迹对称于实轴。
在绘制根轨迹时,只需绘出上半平面的部分,根据对称性,下半平面的部分很容易绘制出来。 自动控制网www.eadianqi.com版权所有
5.实轴上的根轨迹
实轴上的开环零点和开环极点把整个实轴划分为若干线段。这些线段是不是根轨迹的一部分,可以根据幅角条件来判断。只有其右边开环零极点总数为奇数的线段,才能满足根轨迹的幅角条件。所以说,实轴上的根轨迹是那些右边开环零极点个数为奇数的线段。
6.根轨迹的分离点与会合点
两支根轨迹从开环极点出发后相遇又分开的点称为根轨迹的分离点。两支根轨迹相遇后又分开各自趋向终点的点称为根轨迹的会合点。在分离点或会合点上,特征方程必有重根。
分离点或会合点可用下面的方法求取。
系统的特征方程为 自动控制网www.eadianqi.com版权所有
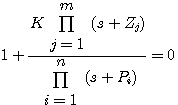 自动控制网www.eadianqi.com版权所有
即 自动控制网www.eadianqi.com版权所有
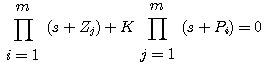 本文来自www.eadianqi.com 本文来自www.eadianqi.com
上式可简化为 自动控制网www.eadianqi.com版权所有
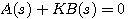 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
式中A(s)和B(s)是不含可变参数K的表达式。解方程 本文来自www.eadianqi.com
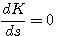 (3.154) 本文来自www.eadianqi.com (3.154) 本文来自www.eadianqi.com
即可求出分离点或会合点。但方程(3.154)的解不一定都是分离点或会合点。经检验,这些点若在根轨迹上,则为分离点或会合点。若不在根轨迹上,此时对应的K一般为负值,则不是分离点或会合点。绝大多数分离点或会合点都分布在实轴上。实轴以外的分离点或会合点则以共轭复数形式成对出现。
7.根轨迹的出射角与入射角
系统存在复数开环零点和开环极点时,必须知道根轨迹从开环复数极点出射的方向或进入到开环零点的方向。
出射角(入射角)是根轨迹在开环复数零极点上切线的方向角,可以根据根轨迹的幅角条件求出。根据式(3.150)可得 本文来自www.eadianqi.com
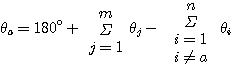 (3.155) (3.155) 本文来自www.eadianqi.com
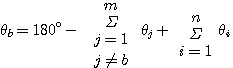 (3.156) 本文来自www.eadianqi.com (3.156) 本文来自www.eadianqi.com
上两式中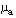 为出射角, 为出射角,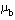 为入射角, 为入射角,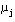 和 和 是所有开环零极点(不包括所求的零极点)指向所求开环复数极点或开环复数零点的矢量与实轴正方向的夹角。 是所有开环零极点(不包括所求的零极点)指向所求开环复数极点或开环复数零点的矢量与实轴正方向的夹角。
8.根轨迹与虚轴的交点
s平面的虚轴是控制系统稳定与不稳定的分界线。根轨迹通过虚轴,系统的稳定性就会发生变化。所以,确定根轨迹与虚轴的交点非常重要。
根轨迹在虚轴上,则s=j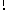 ,将其代入特征方程 自动控制网www.eadianqi.com版权所有 ,将其代入特征方程 自动控制网www.eadianqi.com版权所有
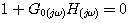 自动控制网www.eadianqi.com版权所有
再令特征方程的实部和虚部都为零,可以得到两个方程:实部方程和虚部方程。求解这两个方程,可得到根轨迹与虚轴的交点和对应的K值。
利用上述8条绘制根轨迹的规则,可以较方便地做出系统的根轨迹图。下面,通过一些实例,进一步了解根轨迹的作图规则。
例17 控制系统的开环传递函数为 自动控制网www.eadianqi.com版权所有
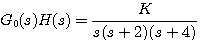 本文来自www.eadianqi.com
试绘制K从零到无穷大变化时系统的根轨迹。
解 (1)系统为三阶系统,根轨迹共有3条分支。
(2)根轨迹的起点为0,-2,-4,图3.29中用 表示开环极点。根轨迹无开环零点,三支根轨迹均终止于无穷远处。 表示开环极点。根轨迹无开环零点,三支根轨迹均终止于无穷远处。
(3)终止于无穷远处的根轨迹的三条渐近线与实轴正方向的夹角和与实轴的交点为 本文来自www.eadianqi.com
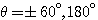 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
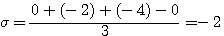 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
(4)根轨迹在实轴上的部分是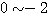 , ,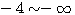 两个线段。 两个线段。
(5)分离点。
特征方程 本文来自www.eadianqi.com
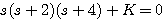 本文来自www.eadianqi.com 本文来自www.eadianqi.com
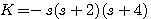 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
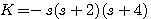 本文来自www.eadianqi.com
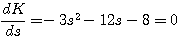 本文来自www.eadianqi.com
求得: 本文来自www.eadianqi.com
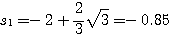 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
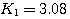 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
 本文来自www.eadianqi.com 本文来自www.eadianqi.com
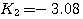
|
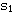 和
和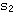 都成为共轭复数。 本文来自www.eadianqi.com
都成为共轭复数。 本文来自www.eadianqi.com
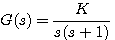
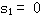
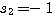
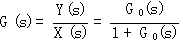
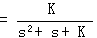
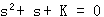
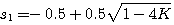 本文来自www.eadianqi.com
本文来自www.eadianqi.com 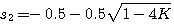
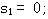
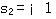 ,与开环极点的位置相同。
,与开环极点的位置相同。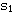 ,
,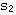 均为负实数,分布在0到-1之间,随K从零开始逐渐增大,
均为负实数,分布在0到-1之间,随K从零开始逐渐增大,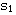 和
和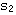 也从开环极点的位置开始逐渐接近。
也从开环极点的位置开始逐渐接近。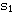 =
=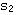 =-0.5,两个闭环极点重合。
=-0.5,两个闭环极点重合。 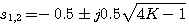
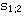 具有相同的负实部,且为常数,而虚部则随K的增加其绝对值也增加。图3.28给出了系统的特征根在K从零变化到无穷大时,相应位置的变化情况。
具有相同的负实部,且为常数,而虚部则随K的增加其绝对值也增加。图3.28给出了系统的特征根在K从零变化到无穷大时,相应位置的变化情况。 1/4时,根轨迹进入复平面,说明系统的单位阶跃响应由单调变化转变为振荡。从图还可以看出,不论K怎样变化,系统始终是稳定的。因为全部根轨迹都分布在s平面左半边。
1/4时,根轨迹进入复平面,说明系统的单位阶跃响应由单调变化转变为振荡。从图还可以看出,不论K怎样变化,系统始终是稳定的。因为全部根轨迹都分布在s平面左半边。 
 (3.145) 本文来自www.eadianqi.com
(3.145) 本文来自www.eadianqi.com  为系统前向通道传递函数,H(s)为系统反馈通道传递函数。上式可改写为
为系统前向通道传递函数,H(s)为系统反馈通道传递函数。上式可改写为 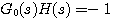 (3.146)
(3.146) 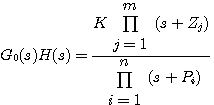 (3.147) 本文来自www.eadianqi.com
(3.147) 本文来自www.eadianqi.com 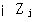 称为开环零点,
称为开环零点,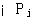 称为开环极点。
称为开环极点。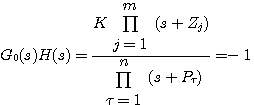 (3.148)
(3.148) 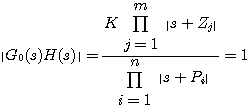 (3.149)
(3.149) 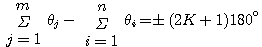 ,
, 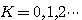 (3.150)
(3.150) 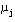 是矢量
是矢量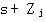 与实轴正方向的夹角,
与实轴正方向的夹角,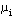 是矢量
是矢量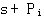 与实轴正方向的夹角。我们称式(3.149)为根轨迹的幅值条件,式(3.150)为根轨迹的幅角条件。凡在根轨迹上的点都是系统特征方程的根,都必须同时满足根轨迹的幅值条件和幅角条件。这两个条件统称为根轨迹的基本条件。
与实轴正方向的夹角。我们称式(3.149)为根轨迹的幅值条件,式(3.150)为根轨迹的幅角条件。凡在根轨迹上的点都是系统特征方程的根,都必须同时满足根轨迹的幅值条件和幅角条件。这两个条件统称为根轨迹的基本条件。  (3.151) 自动控制网www.eadianqi.com版权所有
(3.151) 自动控制网www.eadianqi.com版权所有 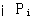 时才会是无穷大。根轨迹的起点是K=0时的根轨迹,所以说根轨迹起始于开环极点。
时才会是无穷大。根轨迹的起点是K=0时的根轨迹,所以说根轨迹起始于开环极点。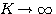 时,方程右边为零,而方程左边只有在
时,方程右边为零,而方程左边只有在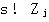 时才会为零。所以可以说根轨迹终止于开环零点。控制系统中,若n>m,m条根轨迹终止于开环零点,还有(n-m)条根轨迹则终止于无穷远处。这时因为,当
时才会为零。所以可以说根轨迹终止于开环零点。控制系统中,若n>m,m条根轨迹终止于开环零点,还有(n-m)条根轨迹则终止于无穷远处。这时因为,当 时,由于n>m,同样有
时,由于n>m,同样有 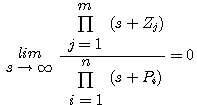
 时,沿渐近线变化。渐近线确定了终止于无穷远处的根轨迹的变化方向。
时,沿渐近线变化。渐近线确定了终止于无穷远处的根轨迹的变化方向。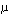 为
为 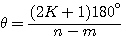
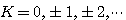 (3.152)
(3.152) 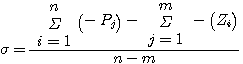 (3.153)
(3.153) 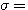 (所有开环极点之和-所有开环零点之和)/n-m 本文来自www.eadianqi.com
(所有开环极点之和-所有开环零点之和)/n-m 本文来自www.eadianqi.com 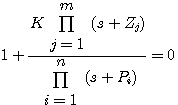
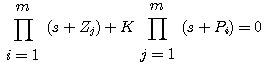
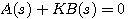 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 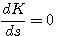 (3.154) 本文来自www.eadianqi.com
(3.154) 本文来自www.eadianqi.com 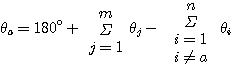 (3.155)
(3.155) 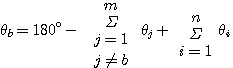 (3.156)
(3.156) 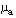 为出射角,
为出射角,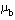 为入射角,
为入射角,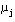 和
和 是所有开环零极点(不包括所求的零极点)指向所求开环复数极点或开环复数零点的矢量与实轴正方向的夹角。
是所有开环零极点(不包括所求的零极点)指向所求开环复数极点或开环复数零点的矢量与实轴正方向的夹角。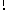 ,将其代入特征方程 自动控制网www.eadianqi.com版权所有
,将其代入特征方程 自动控制网www.eadianqi.com版权所有 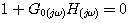
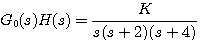
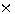 表示开环极点。根轨迹无开环零点,三支根轨迹均终止于无穷远处。
表示开环极点。根轨迹无开环零点,三支根轨迹均终止于无穷远处。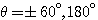 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 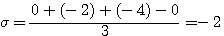 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 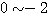 ,
,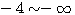 两个线段。
两个线段。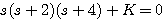
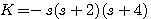 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 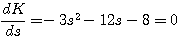
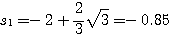
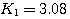 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有  本文来自www.eadianqi.com
本文来自www.eadianqi.com