|
Ⅰ型系统
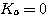 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
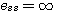 (3.104) (3.104) 本文来自www.eadianqi.com
对Ⅱ型系统 自动控制网www.eadianqi.com版权所有
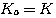 本文来自www.eadianqi.com 本文来自www.eadianqi.com
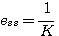 (3.105) 自动控制网www.eadianqi.com版权所有 (3.105) 自动控制网www.eadianqi.com版权所有
K为系统的开环放大系数。
在抛物线函数输入下,0型、Ⅰ型系统都不能使用。Ⅱ型系统则是有差的。若要消除稳态误差,必须选择Ⅲ 型以上的系统。但系统中积分环节太多,动态特性就会变坏,甚至使系统变得不稳定。工程上很少应用Ⅱ型以上的系统。表3.2给出了典型输入函数作用下各型系统的稳态误差。
从以上讨论中可以得出结论:积分环节具有消除稳态误差的作用。这就是许多控制系统中引入积分环节的原因。
误差系数 是利用拉普拉斯变换终值定理得出的,它只是时间趋于无穷大时的值,因此是静态误差系数,它们并不反映误差随时间变化的情况。 自动控制网www.eadianqi.com版权所有 是利用拉普拉斯变换终值定理得出的,它只是时间趋于无穷大时的值,因此是静态误差系数,它们并不反映误差随时间变化的情况。 自动控制网www.eadianqi.com版权所有
3.5.3 扰动作用下的稳态误差
以上我们讨论了控制系统对给定值信号的稳态误差。在控制系统受到扰动时,即使给定值不变,也会产生稳态误差。系统的元件受环境影响、老化、磨损等会使系统特性发生变化,也可以产生稳态误差。系统在扰动作用下的稳态误差大小反映了系统抗干扰的能力。
图3.24是一个控制系统的结构图。我们现在来讨论这个系统在扰动d(t)作用下的稳态误差。按叠加原理,我们假定R(s)=0,系统中只有扰动输入。系统在扰动作用下的输出为 自动控制网www.eadianqi.com版权所有
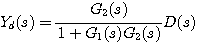 自动控制网www.eadianqi.com版权所有
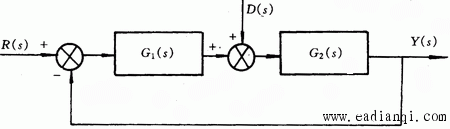
图3.24 控制系统结构图 自动控制网www.eadianqi.com版权所有
误差为 本文来自www.eadianqi.com
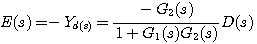 本文来自www.eadianqi.com 本文来自www.eadianqi.com
利用拉普拉斯变换的终值定理得 本文来自www.eadianqi.com
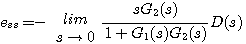 (3.106) 自动控制网www.eadianqi.com版权所有 (3.106) 自动控制网www.eadianqi.com版权所有
值得说明的是,扰动稳态误差与干扰的作用点有关。所以式(3.106)只适用图3.24所示的系统。
若要求系统在给定值输入和扰动输入同时作用下的稳态误差,只要将二者叠加就可以了。
系统在扰动作用下的稳态误差也是系统的一项重要稳态特性指标。
例6 单位反馈系统前向通道的传递函数为 本文来自www.eadianqi.com
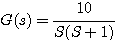 自动控制网www.eadianqi.com版权所有
求系统在输入信号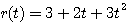 作用下的稳态误差。 作用下的稳态误差。
解 可以根据叠加原理分别求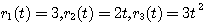 的稳态误差。 的稳态误差。
本系统为Ⅰ型系统, =3为阶跃函数, =3为阶跃函数,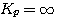 。因此有 。因此有 本文来自www.eadianqi.com
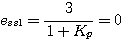 本文来自www.eadianqi.com
 为斜坡函数,稳态速度误差系数 为斜坡函数,稳态速度误差系数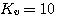 ,由此得到 自动控制网www.eadianqi.com版权所有 ,由此得到 自动控制网www.eadianqi.com版权所有
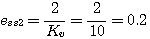 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
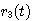 为抛物线函数,稳态加速度误差系数 为抛物线函数,稳态加速度误差系数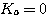 ,因此 ,因此 本文来自www.eadianqi.com
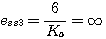 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
系统的稳态误差为 本文来自www.eadianqi.com
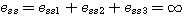 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
|
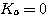
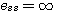 (3.104)
(3.104) 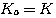 本文来自www.eadianqi.com
本文来自www.eadianqi.com 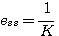 (3.105)
(3.105)  是利用拉普拉斯变换终值定理得出的,它只是时间趋于无穷大时的值,因此是静态误差系数,它们并不反映误差随时间变化的情况。
是利用拉普拉斯变换终值定理得出的,它只是时间趋于无穷大时的值,因此是静态误差系数,它们并不反映误差随时间变化的情况。 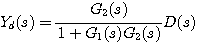

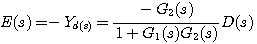 本文来自www.eadianqi.com
本文来自www.eadianqi.com 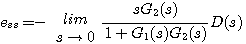 (3.106) 自动控制网www.eadianqi.com版权所有
(3.106) 自动控制网www.eadianqi.com版权所有 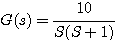
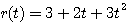 作用下的稳态误差。
作用下的稳态误差。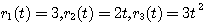 的稳态误差。
的稳态误差。 =3为阶跃函数,
=3为阶跃函数,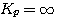 。因此有
。因此有 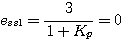
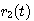 为斜坡函数,稳态速度误差系数
为斜坡函数,稳态速度误差系数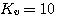 ,由此得到
,由此得到 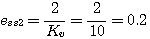
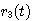 为抛物线函数,稳态加速度误差系数
为抛物线函数,稳态加速度误差系数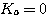 ,因此
,因此 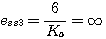 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 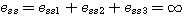 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有