|
奈氏判据是用频率特性来判断系统稳定性的方法,即用开环奈氏图来判断闭环系统的稳定性。它是判别稳定性的图解法,是一种几何判据。 本文来自www.eadianqi.com
一、奈氏稳定判据 本文来自www.eadianqi.com
闭环系统 本文来自www.eadianqi.com 考虑上图所示的闭环系统,其闭环传递函数为 自动控制网www.eadianqi.com版权所有
从稳定的充分必要条件出发,发现闭环传递函数的分母 设一辅助函数, 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
可看出,F(s)的极点即开环传递函数的极点,而F(s)的零点即闭环传递函数的极点。奈奎斯特稳定判据正是将开环频率响应 3、奈奎斯特稳定判据的陈述 本文来自www.eadianqi.com
※ 绘制w从 ※ 根据曲线包围(-1,j0)点的次数和方向,求出N的大小和正负。 自动控制网www.eadianqi.com版权所有
N——w从 自动控制网www.eadianqi.com版权所有
数。
本文来自www.eadianqi.com 当N>0时,按逆时针方向包围的情况。 自动控制网www.eadianqi.com版权所有 当N<0时,按顺时针方向包围的情况。 自动控制网www.eadianqi.com版权所有 当N=0时,表示曲线不包围(-1,j0)点。 自动控制网www.eadianqi.com版权所有
N求法:从(-1,j0)点向 自动控制网www.eadianqi.com版权所有 3600折算N=1,转过-3600折算-1。 本文来自www.eadianqi.com ※ 由给定的开环传递函数确定开环右极点数P,P为正整数或0。 自动控制网www.eadianqi.com版权所有 ※ 由Z=P-2N确定系统的稳定性。 本文来自www.eadianqi.com Z为闭环右极点的个数,其为正整数或0 自动控制网www.eadianqi.com版权所有 系统稳定时,Z=0,即P=2N 本文来自www.eadianqi.com
※ 若 例:已知系统开环传递函数 自动控制网www.eadianqi.com版权所有
应用Nyquist判据判别闭环系统的稳定性 自动控制网www.eadianqi.com版权所有
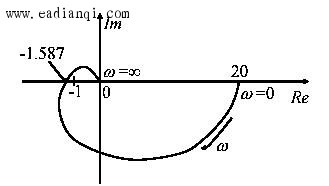
其奈氏曲线为: 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
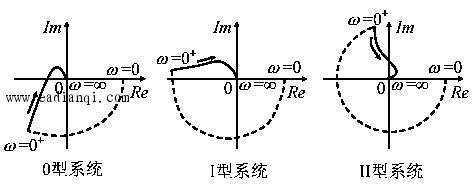
由图可见,开环Nyquist曲线顺时针包围(-1,j0)点一圈,即N=-1: 本文来自www.eadianqi.com 而开环特征根全部位于左半s平面,即P=0,由Nyquist判据知,系统闭环不稳定。 本文来自www.eadianqi.com ※※补充:当系统含有积分环节时,其开环奈氏曲线不封闭,此时需作辅助线。即按常规方法作出ω由0+→ ∞变化时的Nyquist曲线后,从G(j0)开始,以∞的半径顺时针补画v90 °的圆弧(辅助线)得到完整的Nyquist曲线。显然,对于最小相位系统,其辅助线的起始点始终在无穷远的正实轴上。 本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有
|
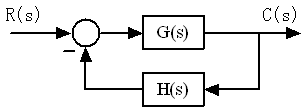
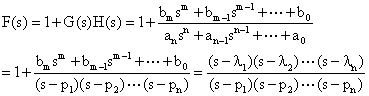
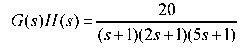
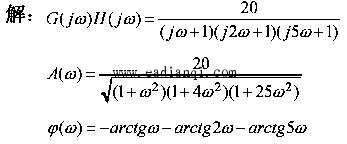
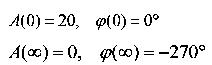 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有