|
该判据不直接对特征方程式求解,而由特征方程中的已知系数,间接地判别出方程的根是否具有负实部,再判稳定性—又称代数稳定性判据。 自动控制网www.eadianqi.com版权所有 一、胡尔维茨稳定判据 自动控制网www.eadianqi.com版权所有
将系统的特征方程式写成: 系统稳定的充要条件是: 自动控制网www.eadianqi.com版权所有 1)系统的特征方程式的各项系数全部为正值,即ai=0 自动控制网www.eadianqi.com版权所有 2)由系统特征方程各项系数组成的主行列式及其各顺序主子式全部大于零。 本文来自www.eadianqi.com 满足这两个条件的系统是稳定的,否则系统是不稳定的。 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有
在实际中,为了计算简化,可计算半数的行列式。 自动控制网www.eadianqi.com版权所有
例:系统的特征方程为: 解:由特征方程知:1)ai=0 本文来自www.eadianqi.com
2)
所以,不满足胡尔维茨行列式,系统不稳定。 本文来自www.eadianqi.com 二、劳斯判据 本文来自www.eadianqi.com
当系统特征方程阶次越高,利用胡氏判据时,行列式计算工作量越大,所以高阶时,可用劳斯判据判别系统的稳定性。 本文来自www.eadianqi.com
有关劳斯判据自身的数学论证,从略。 本文来自www.eadianqi.com 本节主要介绍该判据有关的结论及其在判别控制系统稳定性方面的应用。 自动控制网www.eadianqi.com版权所有 劳斯判据步骤如下: 自动控制网www.eadianqi.com版权所有 1)列出系统特征方程: 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 检查各项系数是否大于0,若是,进行第二步。 本文来自www.eadianqi.com 可见,ai>0 (i=0,1,2,…,n),是满足系统稳定的必要条件。 本文来自www.eadianqi.com
2)按系统的特征方程式列写劳斯表 本文来自www.eadianqi.com
注意:在上述计算过程中,为了简化数学运算,可以用一个正整数去除或乘某一整行,这时并不改变系统 自动控制网www.eadianqi.com版权所有 稳定性的结论。自动控制网www.eadianqi.com版权所有 3)考察劳斯阵列表中第一列各数的符号,如果第一列中各数a0、a1、b1、c1、……的符号相同,则表示系统具有正实部特征根的个数等 本文来自www.eadianqi.com 于零,系统稳定;如果符号不同,系统不稳定,且符号改变的次数等于系统具有的正实部特征根的个数。 自动控制网www.eadianqi.com版权所有 通常a0 > 0,因此,劳斯稳定判据可以简述为劳斯阵列表中第一列的各数均大于零。 自动控制网www.eadianqi.com版权所有 如果劳斯表中第一列系数的符号有变化,其变化的次数等于该特征方程式的根在S的右半平面上的个数,相应的系统为不稳定。 自动控制网www.eadianqi.com版权所有 例 已知一调速系统的特征方程式为 自动控制网www.eadianqi.com版权所有
试用劳斯判据判别系统的稳定性。 本文来自www.eadianqi.com 解:列劳斯表 自动控制网www.eadianqi.com版权所有
由于该表第一列系数的符号变化了两次,所以该方程中有二个根在S的右半平面,因而系统是不稳定的。 自动控制网www.eadianqi.com版权所有 例 已知某调速系统的特征方程式为 本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有
求该系统稳定的K值范围。 本文来自www.eadianqi.com
解:列劳斯表 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 由劳斯判据可知,若系统稳定,则劳斯表中第一列的系数必须全为正值。 自动控制网www.eadianqi.com版权所有 可得: 本文来自www.eadianqi.com
※※ 劳斯判据特殊情况 本文来自www.eadianqi.com 在应用劳斯判据时,有可能会碰到以下两种特殊情况。 自动控制网www.eadianqi.com版权所有
· 劳斯表某一行中的第一项等于零,而该行的其余各项不等于零或没有余项,这种情况的出现使劳斯表无法继续往下排列。解决的办法是以一个很小的正数
若劳斯表第一列中系数的符号有变化,其变化的次数就等于该方程在S右半平面上根的数目,相应的系统为不稳定。如果第一列
例 已知系统的特征方程式为 解:列劳斯表 本文来自www.eadianqi.com
由于表中第一列 自动控制网www.eadianqi.com版权所有
·劳斯表中出现全零行 自动控制网www.eadianqi.com版权所有
则表示相应方程中含有一些大小相等符号相反的实根或共轭虚根。这种情况,可利用系数全为零行的上一行系数构造一个辅助多项式,并以这个辅助多项式导数的系数来代替表中系数为全零的行。完成劳斯表的排列。这些大小相等、径向位置相反的根可以通过求解这个辅助方程式得到,而且其根的数目总是偶数的。例如,一个控制系统的特征方程为 自动控制网www.eadianqi.com版权所有
列劳斯表 本文来自www.eadianqi.com
由于 本文来自www.eadianqi.com
由上表可知,第一列的系数均为正值,表明该方程在S右半平面上没有特征根。令F(s)=0, 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
求得两对大小相等、符号相反的根 |
 胡尔维茨行列式可列写为:
胡尔维茨行列式可列写为: 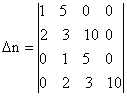
 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有  自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 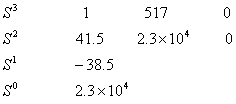 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 
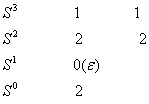 本文来自www.eadianqi.com
本文来自www.eadianqi.com 