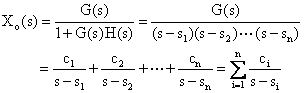|
1、稳定性的概念 稳定性：设一线性定常系统原处于某一平衡状态，若它瞬间受到某一扰动作用而偏离了原来的平衡状态，当此扰动撤消后，系统仍能回到原有的平衡状态，则称该系统是稳定的。反之，若系统对干扰的瞬态响应随着时间的推移而不断扩大或发生持续振荡，则系统为不稳定。 本文来自www.eadianqi.com 由此可知：线形系统的稳定性取决于系统的固有特征（结构、参数），与系统的输入信号无关。 本文来自www.eadianqi.com
2、判别系统稳定性的基本原则 本文来自www.eadianqi.com
对于一般的反馈系统，系统的传递函数为： 自动控制网www.eadianqi.com版权所有
基于稳定性研究的问题是扰动作用去除后系统的运动情况，它与系统的输入信号无关，只取决于系统本身的特征，因而可用系统的脉冲响应函数来描述。 本文来自www.eadianqi.com 设输入信号为单位脉冲信号，则有： 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
通过前面的学习，我们知道，当输入为单位脉冲信号时，若
则系统稳定，若 从<1>式可看出，要想系统稳定，只有当系统的特征根s，全部具有负实部。 本文来自www.eadianqi.com 综上所述，不论系统特征方程的特征根为何种形式，线性系统稳定的充要条件为：所有特征根均为负数或具有负的实数部分；即：所有特 本文来自www.eadianqi.com
征根均在复数平面的左半部分。 本文来自www.eadianqi.com 由于特征根就是系统的极点，因此，线性系统稳定的充要条件也可表述为：系统的极点均在s。平面的左半平面 自动控制网www.eadianqi.com版权所有
显然，稳定性与零点无关。当有一个根落在右半部，系统不稳定。当有根落在虚轴上(不包括原点)，此时为临界稳定，系统产生持续振荡。 自动控制网www.eadianqi.com版权所有 一般情况下，确定系统稳定性的方法有： 本文来自www.eadianqi.com 1）直接计算或间接得知系统特征方程式的根。 自动控制网www.eadianqi.com版权所有 2）确定特征方程的根具有负实部的系统参数的区域。 本文来自www.eadianqi.com 应用第一种类型的两种方法是：1）直接对系统特征方程求解；2）根轨迹法 本文来自www.eadianqi.com 应用第二种类型的两种方法是：1）劳斯-胡尔维茨判据；2）奈氏判据 自动控制网www.eadianqi.com版权所有 |
<1> 
，则系统不稳定。 本文来自www.eadianqi.com