利用开环系统幅相频率特性来判断闭环系统的稳定性。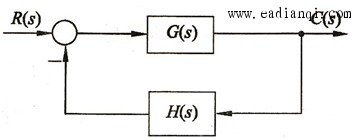 系统开环传递函数  系统闭环传递函数  设: PK为系统的开环传递函数中在[s]平面虚轴右边极点的个数  开环系统稳定 开环系统不稳定P为系统的闭环传递函数中在[s]平面虚轴右边极点的个数  闭环系统稳定 闭环系统不稳定奈奎斯特（Nyquist）稳定判据 自动控制网www.eadianqi.com版权所有 1 即开环系统稳定，闭环系统稳定的充要条件是当ω从-∞→+∞变化时，系统开环幅相频率特性曲线G(jω)H(jω)，不包围(-1，j0)点。 2 即开环系统不稳定，闭环系统稳定的充要条件是当ω从-∞→+∞变化时，系统开环幅相频率特性曲线G(jω)H(jω)，逆时针包围(-1，j0)点PK圈。 3 当ω从-∞→+∞变化时，系统开环幅相频率特性曲线G(jω)H(jω)，通过(-1，j0)点，则闭环系统处于临界稳定状态。  奈奎斯特（Nyquist）稳定判据 设系统开环传递函数为 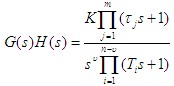 式中υ——开环传递函数中位于原点的极点个数。 本文来自www.eadianqi.com 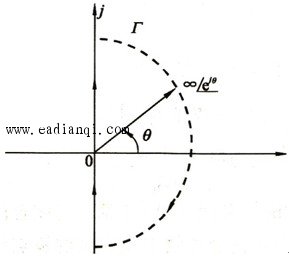 修正后，由四部分组成： 1以原点为圆心,以无限大为半径的大半圆； 2由-j∞到j0-的负虚轴； 3以原点圆心，以ε (ε→0)为半径的从j0-到j0+的小半圆。 4由j0+沿正虚轴到+j∞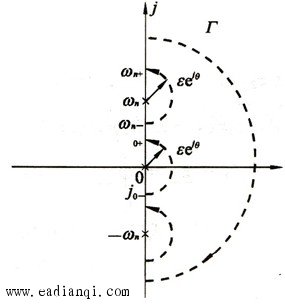；  s平面上有位于坐标原点的υ个极点，奈奎斯特（Nyquist）稳定判据为： 当系统的开环传递函数有υ个极点位于s平面坐标原点时，如果增补开环频率特性曲线G(jω)H(jω)（ω从-∞→+∞）逆时针包围（-1，j0）点的次数 N 等于系统开环右极点个数 PK，则闭环系统稳定，否则系统不稳定。 |