纯粹用试验点的办法手工作图，工作量是十分巨大的，而且对全貌的把握也很困难，于是人们研究根轨迹图的基本法则，以便使根轨迹绘图更快更准。以开环根轨迹增益 为参变量的根轨迹图主要有下列基本法则：1）根轨迹的条数、连续性和对称性 根轨迹的条数=闭环极点个数=开环极点个数 根轨迹具有连续性 根轨迹对称于实轴 2）根轨迹的起点和终点 根轨迹起始于开环极点，终止于开环零点。 3）根轨迹的渐近线 如上所说，当n>m时，根轨迹一定有n－m条趋向无穷远；当n<m时，根轨迹一定有m－n条来自无穷远。根据无穷远处s→∞的特点可以证明：当n≠m时，根轨迹存在|n－m|条渐近线，且渐近线与实轴的夹角为：  所有渐近线交于实轴上的一点，其坐标为 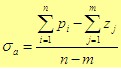 自动控制网www.eadianqi.com版权所有 4）实轴上的根轨迹 实轴上的开环零点和开环极点将实轴分为若干段，对于其中任一段，如果其右边实轴上的开环零、极点总数是奇数，那么该段就一定是根轨迹的一部分。 5）根轨迹的分离角与分离点d 当 从零变到无穷大时，根轨迹可能出现先会合后分离，这样的点称分离点。分离点对应重闭环极点。 分离点d是下列代数方程的解： 必须说明的是，方程只是必要条件而非充分条件，也就是说它的解不一定是分离点，是否是分离点还要看其它规则。 分离角  l为分离的各轨迹条数 6）根轨迹的起始角和终止角 根轨迹离开开环复数极点的切线与正实轴的夹角称为起始角 根轨迹进入开环复数零点的切线与正实轴的夹角称为终止角 用相角条件 根轨迹离开开环复数极点pi的起始角为： 自动控制网www.eadianqi.com版权所有 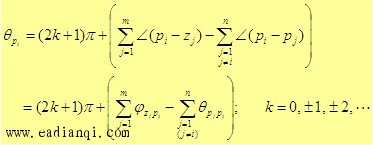 根轨迹进入开环复数零点zi 的终止角为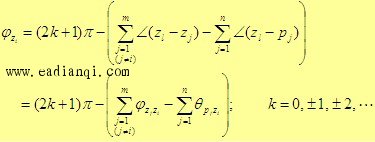：  7）根轨迹与虚轴的交点 根轨迹与虚轴的交点是临界稳定点，该点的坐标jω和增益K*是很重要的，将s=jω代入闭环特征方程，令特征方程的实部和虚部分别等于零，可以解出ω和 。用劳思判据也可以求得。 8）闭环极点和 当n-m≥2时，无论 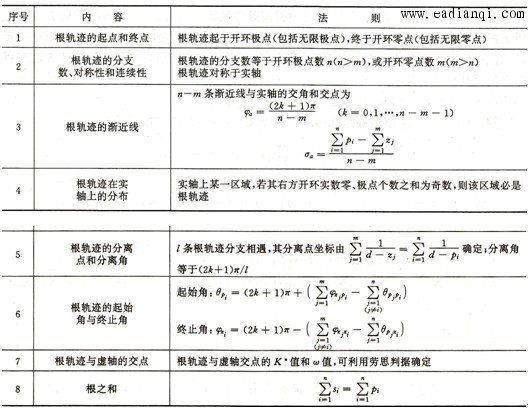取何值，开环n个极点之和总是等于闭环特征方程n个根之和。 自动控制网www.eadianqi.com版权所有 
|