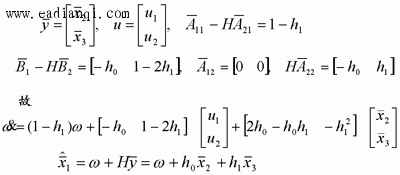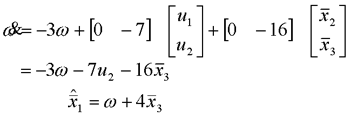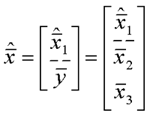|
1、线性定常系统常用反馈结构及其对系统特性的影响 （1）两种常用反馈结构 在系统的综合设计中，两种常用的反馈形式是线性直接状态反馈和线性非动态输出反馈，简称为状态反馈和输出反馈。 1）状态反馈。设有n维线性定常系统   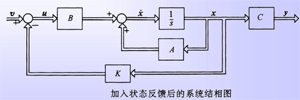  2）输出反馈。系统的状态常常不能全部测量到，因而状态反馈法的应用受到了限制。在此情况下，人们常常采用输出反馈法。输出反馈的目的首先是使系统闭环成为稳定系统，然后在此基础上进一步改善闭环系统性能。 输出反馈有两种形式：一种是将输出量反馈至状态微分，另一种是将输出量反馈至参考输入。 自动控制网www.eadianqi.com版权所有 第一种形式的输出反馈系统的动态方程为  其传递函数矩阵为  输出量反馈至状态微分的系统结构图如图 所示。 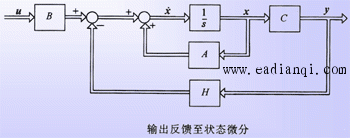 将输出量反馈至参考输入的系统结构图如图 所示。 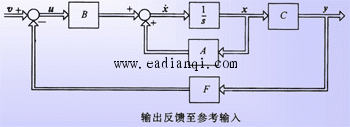 对于输出量反馈至参考输入的系统，当将系统的控制量u取为输出Y的线性函数时，称之为线性非动态输出反馈，常简称为输出反馈，其中 v为 p维参考输入向量，F为p*q 维实反馈增益矩阵。 这是一种最常用的输出反馈。 将上式代入系统动态方程可得输出反馈系统动态方程  其传递函数矩阵为  自动控制网www.eadianqi.com版权所有 不难看出，不管是状态反馈还是输出反馈，都可以改变状态的系数矩阵，但这并不表明二者具有等同的功能。利用状态反馈时，其信息量大而完整，可以在不增加系统维数的情况下，自由地支配响应特性。而输出反馈仅利用了状态变量的线性组合进行反馈，其信息量较小，所引入的补偿装置将使系统维数增加，且难以得到任意的所期望的响应特性。 一个输出反馈系统的性能，一定有对应的状态反馈系统与之等同；但是，对于一个状态反馈系统，却不一定有对应的输出反馈系统与之等同。 （2）反馈结构对系统性能的影响 1）对系统可控怀和可观测性的影响 定理9-1 对于n维线性定常系统，状态反馈的引入不改变系统的可控性，但可能改变系统的可观测性。 定理9-2 对于n维线性定常系统，输出至状态微分反馈的引入不改变系统的可观测性，但可能改变系统的可控性。 定理9-3 对于n维线性定常系统，输出至参考输入反馈的引入能同时不改变系统的可控性和可观测性，即输出反馈系统Sf为可控（可观测）的充分必要条件是被控系统S0为可控（可观测）。 自动控制网www.eadianqi.com版权所有 2）对系统稳定性的影响。状态反馈和输出反馈都能影响系统的稳定性。加入反馈，使得通过反馈构成的闭环系统成为稳定系统，称之为镇定。由于状态反馈具有许多优越性，且输出反馈系统总可以找到与之性能等同的状态反馈系统，故在此只讨论状态反馈的镇定问题。对于线性定常受控系统  如果可以找到状态反馈控制律  其中v为参考输入，使得通过反馈构成的闭环系统  是渐近稳定的，即  的特征值均具有负实部，则称系统实现了状态反馈镇定。定理9-4 当且仅当线性定常系统的不可控部分渐近稳定时，系统是状态反馈可镇定的。 2、系统的极点配置 自动控制网www.eadianqi.com版权所有 状态反馈和输出反馈都能改变闭环系统的极点位置。 所谓极点配置就是利用状态反馈或输出反馈使闭环系统的极点位于所希望的极点位置。由于系统的性能和它的极点位置密切相关，因而极点配置问题在系统设计中是很重要的。 这里需要解决两个问题：一是建立极点可配置的条件，二是确定极点配置所需要的反馈增益矩阵。 （1）极点可配置条件 这里给出的极点可配置条件既适合于单输入－单输出系统，也适合于多输入－多输出系统。 1）利用状态反馈的极点可配置条件 定理9-5 利用状态反馈任意配置闭环极点的充分必要条件是被控系统可控。 本文来自www.eadianqi.com
2）利用输出反馈的极点可配置条件 本文来自www.eadianqi.com
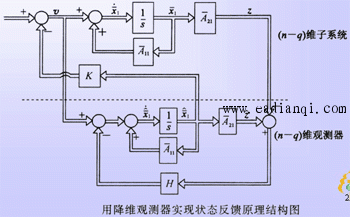
变换矩阵为 自动控制网www.eadianqi.com版权所有 （1）全维状态观测器构成方案 设被控对象动态方程为  可构造一个动态方程与上式相同但用计算机实现的模拟被控系统  上式中  分别为模拟系统的状态向量和输出向量，是被控对象状态向量和输出向量的估值。当模拟系统与被控对象的初始状态向量相同时，在同一输入作用下，有  ，可用  作为状态反馈所需用的信息。但是，被控对象的初始状态可能很不相同，模拟系统中积分器初始条件的设置又只能预估，因而两个系统的初始状态总有差异，即使两个系统的 A,B,C阵完全一样（完全一样通常是不可能的）也存在估计状态与被控对象实际状态的误差  ，难以实现所需要的状态反馈。然而， 的存在必定导致 的存在，而被控系统的输出量总是可以用传感器测量的，于是可根据一般反馈控制原理，使尽快逼近于零，便可以利用 来形成状态反馈。 自动控制网www.eadianqi.com版权所有 按以上原理构成的状态观测器及其实现状态反馈的结构图如图 。 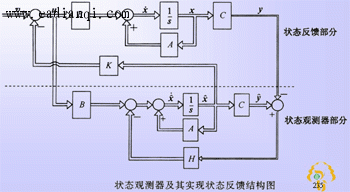 （2）全维状态观测器分析设计 由前图可列出全维状态观测器动态方程   定理9-7 若被控系统(A,B,C)可观测，则其状态可用形如  本文来自www.eadianqi.com
的全维状态观测器给出估值，其中 矩阵按任意配置极点的需要来选择，以决定状态误差衰减的速率。
4、分离特性 自动控制网www.eadianqi.com版权所有 不用状态估值 ，而用状态误差  ，将会使分析研究更加直观方便。由前可得  该式与u,v无关，即 是不可控的，不管施加什么样的控制信号，状态误差总会衰到零，这正是所希望的，是状态观测器所具有的重要性质。对复合系统动态方程式引入非奇异线性变换 则有  由于线性变换后系统传递函数矩阵具有不变性，由上式可导出系统传递函数矩阵 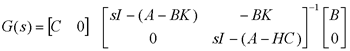 本文来自www.eadianqi.com 利用分块矩阵求逆公式 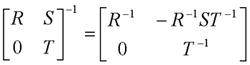 可得  上式正是引入真实状态x作为反馈的状态反馈系统  的传递函数矩阵。这说明复合系统与状态反馈子系统具有相同的传递特性，与观测器部分无关，可用估值状态 代替真实状态x作为反馈。 2n维复合系统导出了(n*n)传递矩阵，这是由于的不可控造成的。线性变换不改变系统特征值，由前易导出  自动控制网www.eadianqi.com版权所有
上式表明复合系统特征值是由状态反馈子系统和全维状态观测器的特征值组合而成，且两部分特征值相互独立，彼此不受影响，故状态反馈矩阵K和输出反馈矩阵H可根据各自的要求来独立进行设计，故有下述分离定理。 本文来自www.eadianqi.com
定理9-8（分离定理） 若被控系统(A,B,C)可控可观测，用状态观测器估值形成状态反馈时，其系统的极点配置和观测器设计可分别独立进行，即K和H阵的设计可分别独立进行。
本文来自www.eadianqi.com |
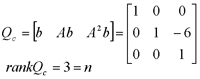
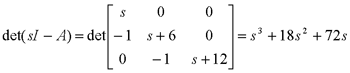
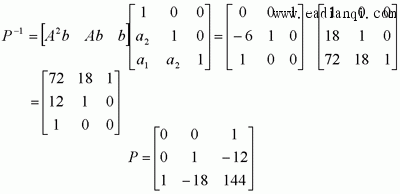
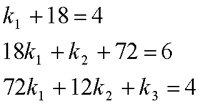
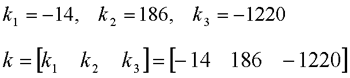
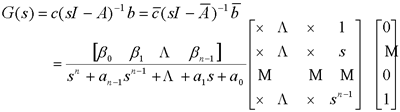
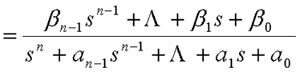自动控制网www.eadianqi.com版权所有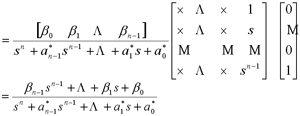 
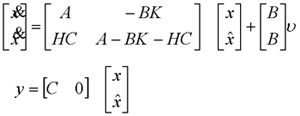
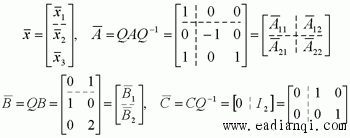
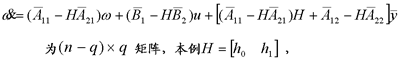的第n列相同，故G(s)与Gk(s) 的分子多项式相同，即闭环系统零点与被控系统零点相同，状态反馈对G(s)的零点没有影响，惟使G(s)的极点改变为闭环系统极点。然而可能有这种情况：
本文来自www.eadianqi.com 
