|
1、李雅普诺夫意义下的稳定性 设系统方程为   的状态Xe称为平衡状态。平衡状态的各分量相对于时间不再发生变化，若已知状态方程，令  所求得的解x，便是平衡状态。线性定常系统  ，其平衡状态满足 ，当A为非奇异矩阵时，系统只有惟一的零解，即只存在一个位于状态空间原点的平衡状态。若A为奇异矩阵，则系统存在有无穷多个平衡状态。对于非线性系统，可能有一个或多个平衡状态。  自动控制网www.eadianqi.com版权所有 该定义的平面几何表示如图所示。 实数δ与ε有关，通常也与t0有关。如果δ与t0无关，则称平衡状态是一致稳定的。 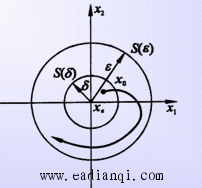 注意：按李雅普诺夫意义下的稳定性定义，当系统作不衰减的振荡运动时，将在平面描绘出一条封闭曲线，但只要不超出s(ε)，则认为是稳定的，这与经典控制理论中线性定常系统稳定性的定义是有差异的。 （3）渐近稳定性 若系统的平衡状态Xe不仅具有李雅普诺夫意义下的稳定性，且有  （4）大范围（全局）渐近稳定性 当初始条件扩展至整个状态空间，且平衡状态均具有渐近稳定性时，称此平衡状态是大范围渐近稳定的。此时，δ->∞，s(δ)->∞。当t->∞时，由状态空间中任一点出发的轨迹都收敛至Xe。 本文来自www.eadianqi.com 对于严格线性的系统，如果它是渐近稳定的，必定是大范围渐近稳定，这是因为线性系统的稳定性与初始条件的大小无关。而对于非线性系统来说，其稳定性往往与初始条件大小密切相关，系统渐近稳定不一定是大范围渐近稳定。 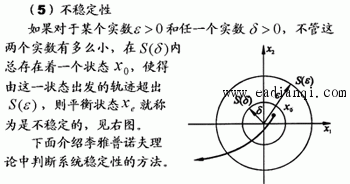 2、李雅普诺夫第一法（间接法） 这是利用状态方程解的特性来判断系统稳定性的方法，它适用于线性定常、线性时变以及非线性函数可线性化的情况。在此仅介绍线性定常系统的特征值判据。 定理9-9 对于线性定常系统  ，有1）系统的每一平衡状态是在李雅普诺夫意义下稳定的充分必要条件是，A的所有特征值均具有非正（负或零）实部，且具有零实部的特征值为A的最小多项式的单根。 本文来自www.eadianqi.com 2）系统的惟一平衡状态Xe=0是渐近稳定的充分必要条件是，A的所有特征值均具有负实部。由于所讨论的为线性定常系统，当其为稳定时必是一致稳定，当其为渐定稳定时必是大范围一致渐近稳定。   正半定性 如果标量函数V(x) 除了原点及某些状态处等于零外，在域S内的所有状态都是正定的，则称V(x)为正半定函数。 负半定性 如果-V(x)是正半定函数，则标量函数V(x)称为负半定函。 不定性 如果在域s内，不论域s多么小，V(x) 既可为正值也可为负值，则标量函数V(x)称为不定函数。   本文来自www.eadianqi.com 定理9-11（定常系统大范围渐近稳定判别定理1） 对于定常系统   定理9-12（定常系统大范围渐近稳定判别定理2） 对于定常系统，如果存在一个具有连续一阶导数的标量函数V(x),V(0=0) ，并且对状态空间X中的一切非零点x满足如下条件：     4、线性定常系统的李雅普诺夫稳定性分析 下面介绍李雅普诺夫第二法在线性定常系统稳定性分析中的应用。 自动控制网www.eadianqi.com版权所有 （1）线性定常连续系统渐近稳定的判别   由于使用中常选取Q阵为单位阵或对角线阵，比起先选P阵再检验Q阵要方便得多，所以在判定系统的稳定性时常利用下述定理： 定理9-14 线性定常系统  的原点平衡状态Xe=0为渐近稳定的充分必要条件是，对于任意给定的一个正定对称矩阵Q，有惟一的正定对称矩阵P使式  成立。上述定理的实质是给出了矩阵A的所有特征值均具有负实部的充分必要条件。  本文来自www.eadianqi.com 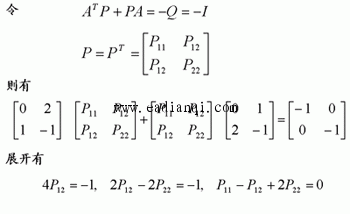  例： 试用李雅普诺夫方程确定使下图所示系统渐近稳定的K值范围  解： 由图示状态变量可列写状态方程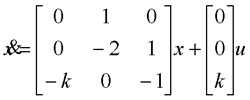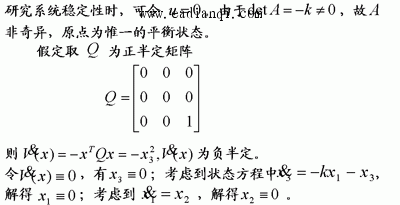      
|