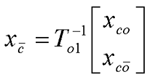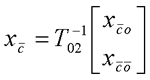|
1、状态空间表达式的线性变换 设系统动态方程为 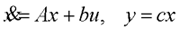 令 令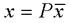 式中P非奇异线性变换矩阵,它将x变换为 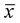 ,变换后的动态方程为 ,变换后的动态方程为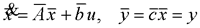 式中 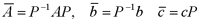 并称为对系统进行变换。线性变换的目的在于使 并称为对系统进行变换。线性变换的目的在于使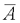 阵规范化, 并不会改变系统的原有性质,故称为等价变换。分析计算后,再引入反变换关系 阵规范化, 并不会改变系统的原有性质,故称为等价变换。分析计算后,再引入反变换关系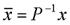 ,得出最终结果。 ,得出最终结果。下面概括给出本章中常用的几种线性变换关系。 (1)化阵为对角型 1)设A阵为任意形式的方阵,且有n个互异实数特征值λ1,λ2,∧,λn,则可由非奇异线性变换化为对角阵∧。 本文来自www.eadianqi.com       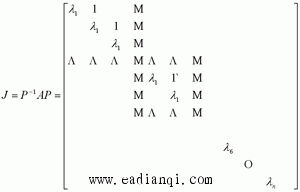 J中虚线示出存在两上约当块,其中
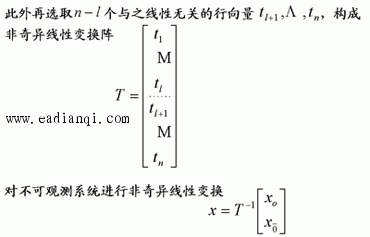
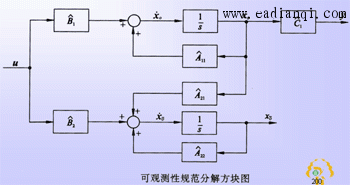
在前面研究状态空间表达式的建立问题时,曾得出单输入线性定常系统状态方程的可控标准型:  与该状态方程对应的可控性矩阵 是一个右下三角阵,其主对角线元素均为1,故detS≠0,系统一定可控,这就是形如上式中A,b的称为可控标准型名称的由来。其可控性矩阵S形如 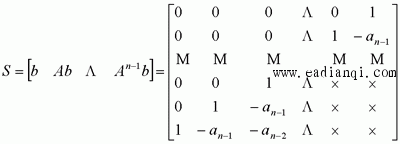 一个可控系统,当A,b不具有可控标准型,一定可以选择适当的变换化为可控标准型。设系统状态方程为  进行 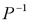 变换,即令 变换,即令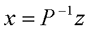 变换为 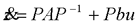 要求  自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有 下面具体推导变换矩阵P: 设变换矩阵P为 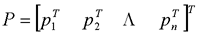 根据A阵变换要求,P应满足变换要求,有 根据A阵变换要求,P应满足变换要求,有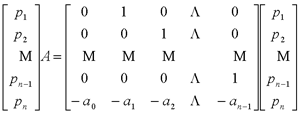 展开为 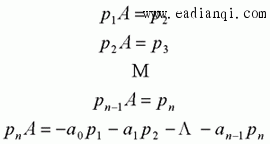 经整理有 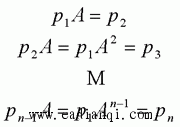 由此可得变换矩阵  又根据b阵变换要求,P应有 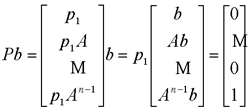 即 即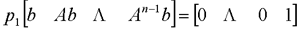 故 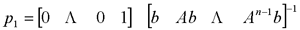 该式表明p1是可控性矩阵的逆阵的最后一行。于是可得出变换矩阵 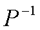 的求法如下: 本文来自www.eadianqi.com 的求法如下: 本文来自www.eadianqi.com 1)计算可控性矩阵 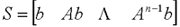 ; ;2)计算可控性矩阵的逆阵 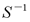 ,设一般形式为 ,设一般形式为 3)取出 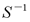 的最后一行(即第n行)构成p1行向量 的最后一行(即第n行)构成p1行向量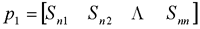  2、对偶原理 在研究系统的可控性和可观测性时,利用对偶原理常常带来许多方便。  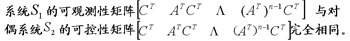 应用对偶原理,把可观测的单输入-单输出系统化为可观测标准型的问题转化为将其对偶系统化为可控标准型的问题。设单输入-单输出系统动态方程为 自动控制网www.eadianqi.com版权所有  系统可观测,但A,c不是可观测标准型。其对偶系统动态方程为 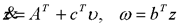 对偶系统一定可控,但不是可控标准型。可利用已知的化为可控标准型,再一次使用对偶原理,便可获得可观测标准型。 下面仅给出其计算步骤:   其中 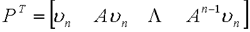 Vn为原系统可观测性矩阵的逆阵中第n行的转置。 3、非奇异线性变换的不变特性 通过研究将会表明,系统经过非奇异线性变换,系统的特征值、传递矩阵、可控性、可观测性等重要性质均保持不变。下面以P变换为例进行论证。 设系统动态方程为 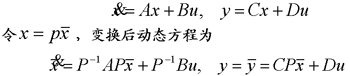 本文来自www.eadianqi.com 本文来自www.eadianqi.com (1)变换后系统特征值不变 变换后系统的特征值为 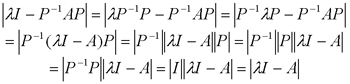 可见,系统变换后与变换前的特征值完全相同,这说明对于非奇异线性变换,系统特征值具有不变性。 (2)变换后系统传递矩阵不变 变换后系统的传递矩阵为 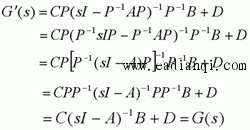 这表明变换前与变换后系统的传递矩阵完全相同,系统的传递矩阵对于非奇异线性变换具有不变性。 (3)变换后系统可控性不变 变换后系统可控性矩阵的秩为 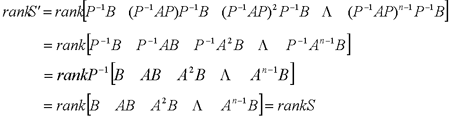 其中,S'为变换后系统的可控性矩阵;S为变换前系统的可控性矩阵。可见,变换后与变换前系统可控性矩阵的秩相等,根据系统可控性的秩判据可知,对于非奇异线性变换,系统的可控性不变。 (4)变换后系统可观测性不变 自动控制网www.eadianqi.com版权所有 设变换后系统的可观测性矩阵为 v',变换前系统的可观测性矩阵为v ,则有 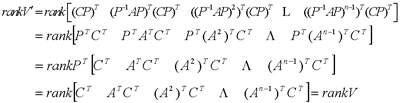 可见,变换后与变换前系统的可观测性矩阵的秩相等,故系统的可观测性不变。 4、线性定常系统的结构分解 从可控性和可观测性出发,状态变量便可分为可控可观测 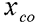 、可控不可观测 、可控不可观测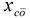 、不可控可观测 、不可控可观测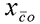 、不可控不可观测 、不可控不可观测 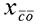 四类。由对应状态变量构成的子空间也分为四类,因而系统也对应分成了四类子系统,称为系统的结构分解,也有的参考文献称此为系统的规范分解。 四类。由对应状态变量构成的子空间也分为四类,因而系统也对应分成了四类子系统,称为系统的结构分解,也有的参考文献称此为系统的规范分解。研究方法是选取一种特殊的线性变换,使原来的状态向量x变换成 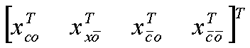 ,相应地使原动态方程中的矩阵A,B,C变换成某种标准构造的形式。 ,相应地使原动态方程中的矩阵A,B,C变换成某种标准构造的形式。 自动控制网www.eadianqi.com版权所有 (1)系统按可控性的结构分解 设不可控系统的动态方程为 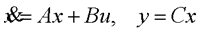   展开规范表达式,有 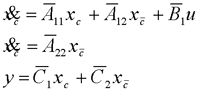 将输出向量进行分解,令Y=Y1+Y2,则可得子系统动态方程,其中可控子系统动态方程为 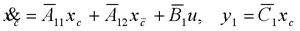 不可控子系统动态方程为 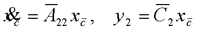 上述系统结构分解方式称之为可控性规范分解,系统方块图如图所示。  系统结构的可控性规范分解具有下列特点: 1)由于 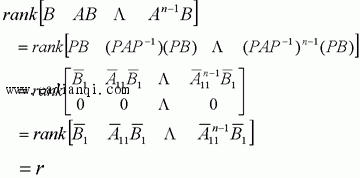 本文来自www.eadianqi.com 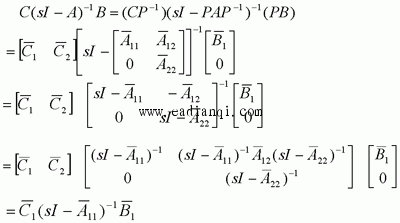
因而R维系统 自动控制网www.eadianqi.com版权所有
2)输入u只能通过可控子系统传递到输出,而与不可控子系统无关,故u至y之间的传递函数矩阵描述不能反映不可控部分的特性,这就从物理意义上进一步说明了可控子系统 自动控制网www.eadianqi.com版权所有
式中T01基于可控子系统的可观测性矩阵来构造。最后对不可控子系统进行可观测性分解,即引入状态变换  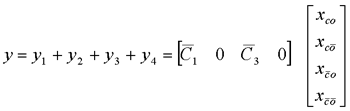 展开上两式,可得可控、可观测子系统动态方程 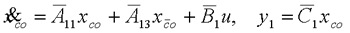 可控、不可观测子系统动态方程 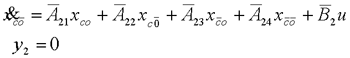 不可控、可观测子系统动态方程   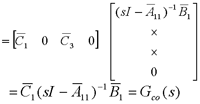 式中“×”表示因比较复杂而未具体写出的矩阵表达式。由前分析可知,整个线性定常系统的传递函数矩阵与可控、可观测子系统的传递函数矩阵相同,这就是说,对于不可控又不可观测的线性定常系统,其输入-输出描述即传递函数矩阵只能描述系统中可控且可观测的那一部分,是对系统结构的一种不完全描述。只有当系统可控且可观测时,输入-输出描述才足以表征系统的结构,即描述是完全的。 |
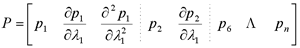
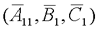 是可控的,并且和系统
是可控的,并且和系统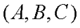 具有相同的传递函数矩阵。如果从传递特性的角度分析系统
具有相同的传递函数矩阵。如果从传递特性的角度分析系统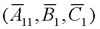 来代替,
来代替,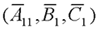 和系统
和系统

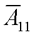 的阶数R<N 。按照上面所述的非奇异线性变换阵
的阶数R<N 。按照上面所述的非奇异线性变换阵 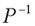 的选取方法,利用计算机进行线性变换计算,可以比较容易地确定系统(A,B,C)的可控性。对于维数较大系统的可控性判别,这是一种较好的方法。
的选取方法,利用计算机进行线性变换计算,可以比较容易地确定系统(A,B,C)的可控性。对于维数较大系统的可控性判别,这是一种较好的方法。 本文来自www.eadianqi.com
本文来自www.eadianqi.com 

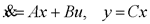 系统的可观测性矩阵为
系统的可观测性矩阵为


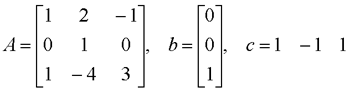
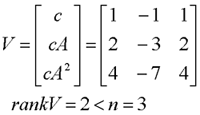


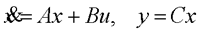
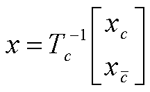
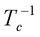 基于系统可控性矩阵来构造。
基于系统可控性矩阵来构造。