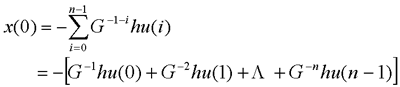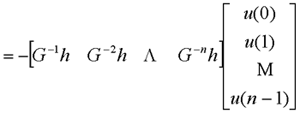|
现代控制理论中用状态方程和输出方程描述系统,输入和输出构成系统的外部变量,而状态为系统的内部变量,这就存在着系统内的所有状态是否可受输入影响和是否可由输出反映的问题,这就是可控性和可观测性问题。如果系统所有状态变量的运动都可以由输入来影响和控制而由任意的初态达到原点,则称系统是可控的,或者更确切地是状态可控的。否则,就称系统是不完全可控的,或简称为系统不可控。相应地,如果系统所有状态变量地任意形式的运动均可由输出完全反映,则称系统是状态可观测的,简称为系统可观测。 例: 给定系统的动态方程为
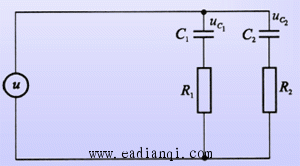
例:下图所示网络,设x1=Uc1,x2=Uc2,输出y=x2。
当R1=R2,C1=C2且初始状态x1(t0)=x2(t0)时,则不论将输入U取为何种形式,对于所有t≥t0,只能是x1(t)≡x2(t),不可能做到x1(t)≠x2(t)。也就是说,输入u能够做到使X1和x2同时转移到任意相同的目标值,但不能将x1和x2分别转移到不同的目标值。这表明此电路不完全可控,简称电路不可控。由于y=x1=x2,故系统可观测。 自动控制网www.eadianqi.com版权所有
1、可控性 本文来自www.eadianqi.com
系统可控: 对于上式所示线性时变系统,如果状态空间中的所有非零状态都是在 本文来自www.eadianqi.com 状态与系统可达: 若存在能将状态x(t0)=0转移到x(tf)=xf的控制作用,则称状态 xf是t0时刻可达的。若xf对所有时刻都是可达的,则称状态xf为完全可达或一致可达。若系统对于状态空间中的每一个状态都是t0时刻可达的,则称该系统是t0时刻状态完全可达的,或简称该系统是t0时刻可达的。 对于线性定常连续系统,可控性与可达性是等价的。但对于离散系统和时变系统,严格地说两者是不等价的。 2、可观测性 可观测性表征状态可由输出完全反映的性能,所以应同时考虑系统的状态方程和输出方程 自动控制网www.eadianqi.com版权所有
其中,A(t),B(t),C(t)和D(t)分别为(n×n),(n×p),(q×n) 和(q×p)的满足状态方程解的存在惟一性条件的时变矩阵。状态方程的解为
3、线性定常连续系统的可控性判据 自动控制网www.eadianqi.com版权所有
下面根据A和B给出系统可控性的常用判据。 格拉姆矩阵判据 线性定常连续系统完全可控的充分必要条件是,存在时刻t1>0,使如下定义的格拉姆矩阵: 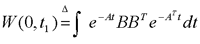 为非奇异。 格拉姆矩阵判据主要用于理论分析。线性定常连续系统可控性的常用判据是直接由矩阵A和B判断可控性的秩判据。 凯莱-哈密顿定理 设阶矩阵的特征多项式为
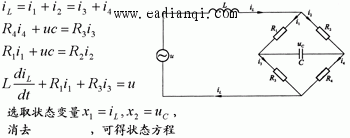
例: 桥式网络如图所示,试用可控性判据判断其可控性。 自动控制网www.eadianqi.com版权所有 解: 该桥式电路的微分方程为 本文来自www.eadianqi.com
其可控性矩阵为 本文来自www.eadianqi.com
可控性矩阵为 自动控制网www.eadianqi.com版权所有
解 可控性判别矩阵为 本文来自www.eadianqi.com
由于这一判据是由波波夫和贝尔维奇首先提出,并由豪塔斯最先指出其可广泛应用性,故称为PBH秩判据。
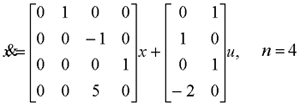
试判别系统的可控性。
PBH特征向量判据 线性定常连续系统完全可控的充分必要条件是,A不能有与B 的所有列相正交的非零左特征向量。即A对的任一特征值λi,使同时满足 本文来自www.eadianqi.com
的特征向量a≡0 。 自动控制网www.eadianqi.com版权所有
则系统完全可控的充分必要条件是,在上式中,不包含元素全为零的行。 自动控制网www.eadianqi.com版权所有
由线性变换化为约当规范型 本文来自www.eadianqi.com
4、输出可控性 自动控制网www.eadianqi.com版权所有
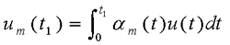 则 则
令 自动控制网www.eadianqi.com版权所有
注意:状态可控性与输出可控性是两个不同的概念,二者没有什么必然的联系。
5、线性定常连续系统的可观测性判据
其中,x为n维状态向量;y为q维输出向量;A和c分别为n*n和q*n的常值矩阵。
为非奇异。 秩判据 线性定常连续系统完全可观测的充分必要条件是 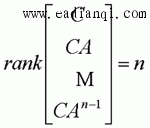 或 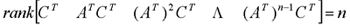 上两式中的矩阵均称为系统可观测性判别阵,简称可观测性阵。 例: 判断下列系统的可观测性: 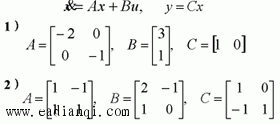 解:1) 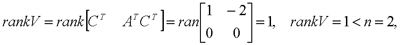 故系统不可观测。 2) 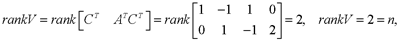 故系统可观测。
6、线性离散系统的可控性和可观测性 自动控制网www.eadianqi.com版权所有 本文来自www.eadianqi.com
可控性和可达性等价的充分必要条件是系统矩阵
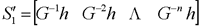 称s'为(n*n)可控性矩阵。由线性方程组解的存在定理可知,当矩阵s1'的秩与增广矩阵[s1',Mx(0)]的秩相等时,方程组有解且为惟一解,否则无解。在x(0)为任意的情况下,使方程线有解的充分必要条件是矩阵s1'满秩,即 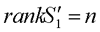
当 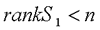 时,系统不可控,表示不存在使任意x(0)转移至x(n)=0的控制。 自动控制网www.eadianqi.com版权所有 时,系统不可控,表示不存在使任意x(0)转移至x(n)=0的控制。 自动控制网www.eadianqi.com版权所有 以上研究了终态为x(n)=0的情况,若令终态为任意给定状态x(n),则状态方程的解变为 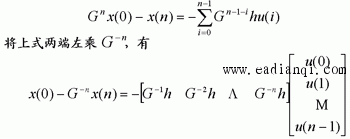   由于初态x()可任意给定,根据解存在定理,矩阵s2' 的秩为n时,方程组才有解。于是多输入线性离散系统状态可控的充分必要条件是
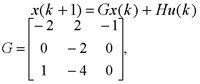 试判断可控性,并研究使x(1)=0的可能性。 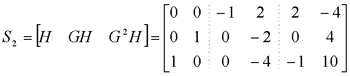 显然,由前三列组成的矩阵的行列式不为零,故系统可控。 一定能求得控制序列使系统由任意初始状态三步内转移到原点。 本文来自www.eadianqi.com 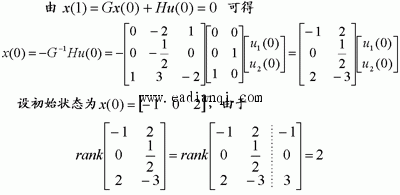    其向量-矩阵形式为 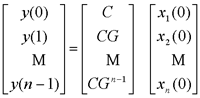 令 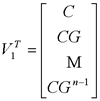  (3)连续动态方程离散化后的可控性和可观测性 一个可控的或可观测的连续系统,当其离散化后并不一定能保持其可控性或可观测性。现举例来说明。 设连续系统动态方程为 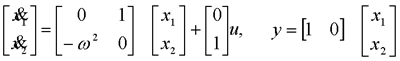 由于系统的状态方程为可控标准型,故一定可控。根据可观测性判据有 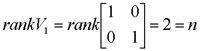 本文来自www.eadianqi.com 本文来自www.eadianqi.com 故系统可观测。 系统的状态转移矩阵为 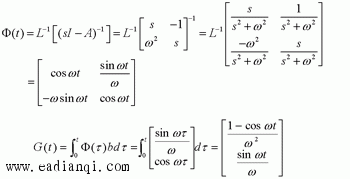 系统离散化后的状态方程为 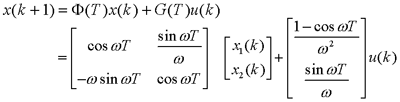 离散化后系统的可控性矩阵为 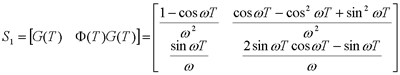 离散化后系统的可观测性矩阵为 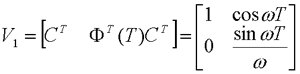 当采样周期时 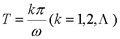 ,可控性矩阵S1和可观测性矩阵V1均出现零行, ,可控性矩阵S1和可观测性矩阵V1均出现零行,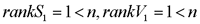 ,系统不可控也不可观测。这表明连续系统可控或可观测时,若采样周期选择不当,对应的离散化系统便有可能不可控或不可观测,也有可能既不可控又不可观测。若连续系统不可控或不可观测,不管采样周期 如何选择,离散化后的系统一定是不可控或不可观测的。 ,系统不可控也不可观测。这表明连续系统可控或可观测时,若采样周期选择不当,对应的离散化系统便有可能不可控或不可观测,也有可能既不可控又不可观测。若连续系统不可控或不可观测,不管采样周期 如何选择,离散化后的系统一定是不可控或不可观测的。
|
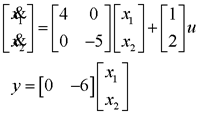


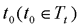 时刻可控的,则称系统在t0时刻是完全可控的,简称系统在t0时刻可控。若系统在所有时刻都是可控的,则称系统是一致可控的。
时刻可控的,则称系统在t0时刻是完全可控的,简称系统在t0时刻可控。若系统在所有时刻都是可控的,则称系统是一致可控的。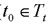 ,如果状态空间中存在一个或一些非零状态在t0时刻是不可控的,则称系统在t0时刻是不完全可控的,也称为系统是不可控的。
,如果状态空间中存在一个或一些非零状态在t0时刻是不可控的,则称系统在t0时刻是不完全可控的,也称为系统是不可控的。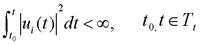
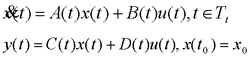
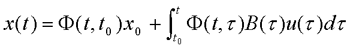


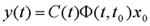
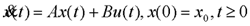

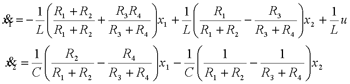
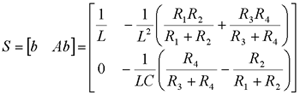





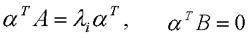

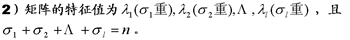


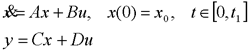

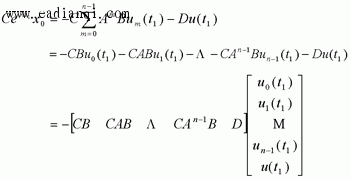
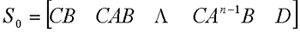
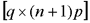
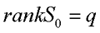
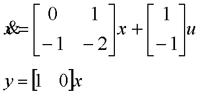
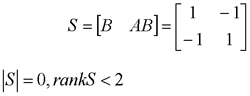

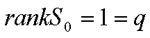
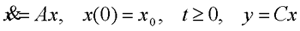
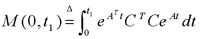




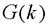 对所有
对所有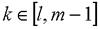 为非奇异;
为非奇异;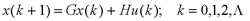
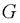 为非奇异。
为非奇异。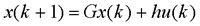

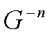 ,则有
,则有