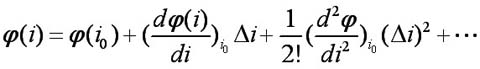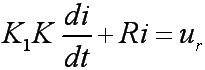|
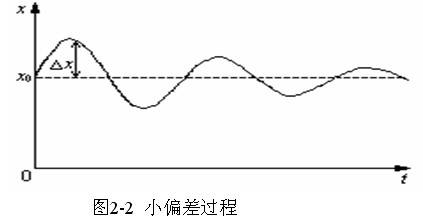
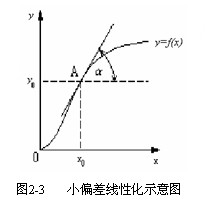
几乎所有元件或系统的运动方程都是非线性的。但对于较小的范围内的运动,把这些元件看作是线性元件,因此可以建立线性微分方程。线性微分方程,满足迭加原理和齐次性。 自动控制网www.eadianqi.com版权所有 研究非线性系统在某一工作点(平衡点)附近的性能,(如图2-2,x0为平衡点,受到扰动后,x(t)偏离x 0,产生Δx(t),Δx(t)的变化过程,表征系统在x0附近的性能) 自动控制网www.eadianqi.com版权所有
可用下述的线性化方法得到的线性模型代替非线性模型来描述系统: 本文来自www.eadianqi.com
设连续变化的非线性函数为y = f(x)。取某平衡状态A为工作点,即y0=f(x0) 。当x=x0+Δx 时,y=y0+Δy ,设函数f(x)在(x0,y0) 连续可微,则在该点附近用泰勒级数展开为: 本文来自www.eadianqi.com
当(x-x0) 很小时,略去高次幂相,则 本文来自www.eadianqi.com
则略去增量符号,可得到在工作点附近的线性化方程 本文来自www.eadianqi.com
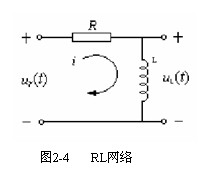
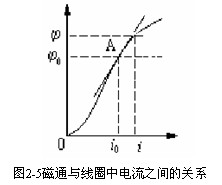
例2-3,设铁芯线圈电路如图2-4所示,其磁通与线圈中电流之间的关系如图2-5所示,试写出以为输入,为输出的微分方程。 自动控制网www.eadianqi.com版权所有
解(1)设铁芯线圈磁通变化时产生的感应电势为: 本文来自www.eadianqi.com
(2)电路微分方程为:
设在平衡点的邻域内, j 对i的各阶导数(直至n+1)是存在的,它可展成泰勒级数: 自动控制网www.eadianqi.com版权所有
(2.8) 本文来自www.eadianqi.com 其中:Δi =i - i 0 自动控制网www.eadianqi.com版权所有
当Δi 足够小时,略去高阶导数
式中 略去增量符号,得 自动控制网www.eadianqi.com版权所有
将式(2.10)代入式(2.7),则把原来非线性数学模型,转化成常系数线性数学模型: 本文来自www.eadianqi.com
在线性化过程中,只考虑泰勒级数中的一次偏量,故式(2.10)又称为一次线性化方程式。 本文来自www.eadianqi.com 总结:要建立整个系统的线性化微分方程式,首先确定系统处于平衡状态时,各元件的工作点;然后列出各元件在工作点附近的偏量方程式,消去中间变量;最后得到整个系统以偏量表示的线性化方程式。 本文来自www.eadianqi.com |
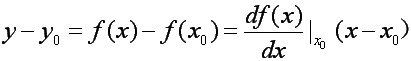
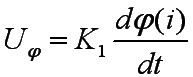 (2.7)
(2.7) 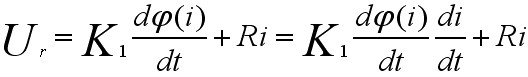 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有