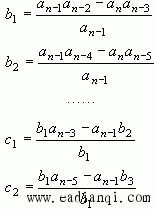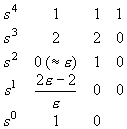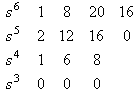|
稳定性是控制系统最重要的问题，也是对控制系统最基本的要求，因为一个控制系统不稳定，就不能正常工作。不稳定的控制系统，当受到内部或外界扰动，如负载或能源的波动、系统参数变化等，系统中各物理量偏离原平衡工作点，并随着时间的推移而发散，即使在干扰消失后也不可能再恢复到原平衡状态。 本文来自www.eadianqi.com
线性定常系统渐近稳定的充要条件 自动控制网www.eadianqi.com版权所有
系统的闭环特征根全部分布S平面的左半部而具有负实部。可见控制系统的稳定性取决于系统本身的结构和参数，与外加输入信号无关。 本文来自www.eadianqi.com 稳定性分析 自动控制网www.eadianqi.com版权所有 判断线性定常系统稳定性的基本方法通常有以下几种： 本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
劳斯稳定判据法 本文来自www.eadianqi.com
设系统特征方程为 本文来自www.eadianqi.com
则可列出如下劳斯计算表 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 表中有关系数计算方法如下： 本文来自www.eadianqi.com
劳斯判据：当且仅当劳斯计算表中第一列各元符号相同时，系统渐近稳定；否则系统不是渐近 自动控制网www.eadianqi.com版权所有 稳定的，且第一列各元符号改变次数等于具有正实部特征根的个数。 本文来自www.eadianqi.com 
劳斯稳定判据法的特殊应用 本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有 解：建立Routh计算表 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
注意，在进行Routh计算表的第三行运算时，出现第一列元素为零而其它各列元素不为零的现象。这时，按Routh法则需要将零元素用趋近于的正数
解：建立Routh计算表 本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有
注意，在建立Routh计算表过程中，若出现某一行元素全部为零现象，则首先需利用该行的上一行的元素构造辅助方程式。
自动控制网www.eadianqi.com版权所有
从Routh计算表看出，第一列各元素的符号均相同而无变化，这说明系统特征方程是在 自动控制网www.eadianqi.com版权所有
|
本文来自www.eadianqi.com 
特征方程法——通过求解特征方程的所有根并判断其是否均具有负实部来决定系统稳定性，该方法也可称作直接法。方程阶次较高时难以应用。 
某行的一个元为零，而其它各元不全为零。解决方法有两种：用很小的正数
代替的一个零元；或用
（要求
）乘原特征方程得新特征方程，再用劳斯判据，因新、原特征方程具有相同的稳定性。 
设某系统的特征方程式为
，试用Routh稳定判据判别系统的稳定性。 
，试用Routh稳定判据判别系统的稳定性。 自动控制网www.eadianqi.com版权所有 
行的元素全部为零，故需利用该行的上一行，即
行中元素构造如下辅助方程式
；其次将辅助方程是各项对变量
求导，得到一个较辅助方程低一阶的新方程式。得
；最后用新方程式的各项系数去代替全零行的元素，并继续进行Routh计算表的运算，直到
行，有Routh计算表 自动控制网www.eadianqi.com版权所有 
和
。具有共轭虚根的系统，理论上认为其具有临界稳定性。