|
利用常用信号Z变换对和Z变换的性质，可以求解复杂信号的Z变换和反变换。总之，掌握Z变换的性质，可以从性质的基本形式、应用该性质的基本思路及应用中应该注意的问题三个方面来掌握。 自动控制网www.eadianqi.com版权所有 Z变换是一种线性变换，它满足叠加原理，即若有: 本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有
那么对于任意常数a、b，Z变换都能满足以下等式： 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com 通常两序列和的Z变换的收敛域为两个相加序列的收敛域的公共区域： 本文来自www.eadianqi.com
如果线性组合中某些零点与极点互相抵消， 则收敛域可能扩大。 自动控制网www.eadianqi.com版权所有 2. 序列的移位 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 位移m可以为正（右移）也可以为负（左移）。 自动控制网www.eadianqi.com版权所有 证： 本文来自www.eadianqi.com
3. 乘以指数序列（Z域尺度变换） 自动控制网www.eadianqi.com版权所有
证： 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
4. X(z)的微分 本文来自www.eadianqi.com
证： 本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有
5. 复序列的共轭 本文来自www.eadianqi.com
证： 本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有 6. 翻褶序列 自动控制网www.eadianqi.com版权所有
证： 本文来自www.eadianqi.com
7. 初值定理 本文来自www.eadianqi.com
对于因果序列x(n)，即x(n)=0, n<0, 有 本文来自www.eadianqi.com 证： 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有
8. 终值定理 本文来自www.eadianqi.com
设x(n)为因果序列，且X(z)=Z［x(n)］的全部极点，除有一个一阶极点可以在z=1 处外，其余都在单位圆内，则 本文来自www.eadianqi.com
证：利用序列的移位性质可得 自动控制网www.eadianqi.com版权所有
再利用x(n)为因果序列可得
分析一下(z-1)X(z)的收敛域。由于X(z)在单位圆上只有在z=1 处可能有一阶极点，函数(z-1)X(z)将抵消掉这个z=1处的可能极点，因此(z-1)X(z)的收敛域将包括单位圆，即在1≤|z|≤∞上都收敛，所以可以取z→1 的极限, 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有
9. 序列卷积（卷积定理） 本文来自www.eadianqi.com
若
自动控制网www.eadianqi.com版权所有
则 自动控制网www.eadianqi.com版权所有 在线性时不变系统中，如果输入为x(n)，系统的单位脉冲响应为h(n)，则输出y(n)是x(n)与h(n)的卷积; 利用卷积定理， 通过求出X(z)和H(z)，然后求出乘积X(z)H(z)的Z反变换，从而可得y(n)。这个定理得到广泛应用。 自动控制网www.eadianqi.com版权所有
10. 序列乘积（复卷积定理） 自动控制网www.eadianqi.com版权所有
若
则 |
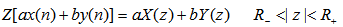
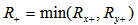自动控制网www.eadianqi.com版权所有 
自动控制网www.eadianqi.com版权所有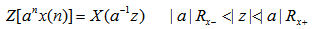 
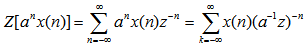
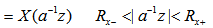
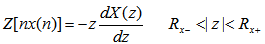
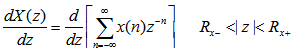交换求和与求导的次序，则得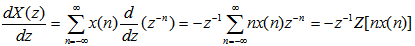 
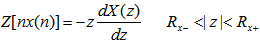
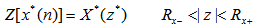式中，符号“*”表示取共轭复数 自动控制网www.eadianqi.com版权所有 
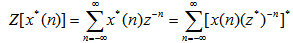自动控制网www.eadianqi.com版权所有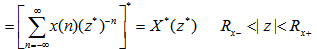 
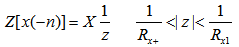
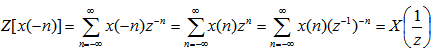本文来自www.eadianqi.com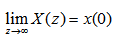 
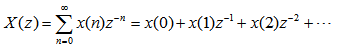
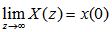
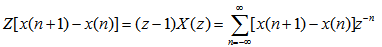自动控制网www.eadianqi.com版权所有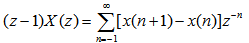 
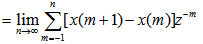自动控制网www.eadianqi.com版权所有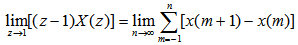 
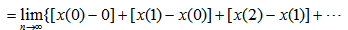
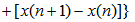
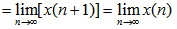
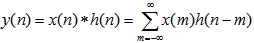自动控制网www.eadianqi.com版权所有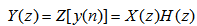 
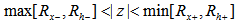
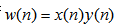自动控制网www.eadianqi.com版权所有 
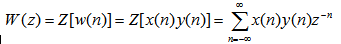本文来自www.eadianqi.com 
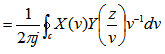自动控制网www.eadianqi.com版权所有