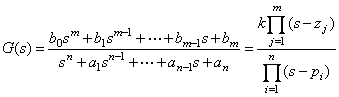|
解微分方程是件困难的工作，经过拉氏变换，变换成代数方程，便于分析和处理。控制系统的复数域数学模型称为传递函数，是经典控制理论的最基本和最重要的概念。 传递函数定义：(P29,倒4行)在初始状态(条件)为零的情况下，输出量的拉氏变换  与输入量的拉氏变换 之比。记为
 及其输入 ，求系统的输出 。 传递函数的性质： (1) 只有线性定常系统具有传递函数； (2) 传递函数反映系统的本质特性，与输入量的具体形式无关； (3) 传递函数表达系统输出量对于系统输入量的响应关系，因此，在进行拉氏变换时，所有初始状态均为零；传递函数与微分方程一一对应； (4) 传递函数是复变量S的有理函数；见定义表达式； 本文来自www.eadianqi.com (5) 传递函数 的拉氏反变换是脉冲响应函数 。脉冲响应函数是指系统输出对单位脉冲输入 的响应，即
列写系统的微分方程； 初始状态为零，对方程两边作拉氏变换； 写出标准的传递函数形式。 传递函数的零点和极点： 在不同应用时，传递函数有相应的标准形式。讨论系统零极点时的形式为
自动控制网www.eadianqi.com版权所有
式中 本文来自www.eadianqi.com |
，
，
，
。 
是分子多项式的零点，称为系统的零点；
是分母多项式的零点，称为系统的极点；极点的个数n，为系统的阶次。