一、二阶系统 自动控制网www.eadianqi.com版权所有
二阶系统的传递函数有如下两种形式:
本文来自www.eadianqi.com
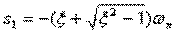 (1)或
(1)或
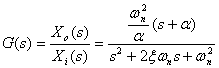 (2)
(2)
其中,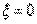 是二阶系统的特征参数,它们表明二阶系统本身的与外界无关的固有特性。一般将式(1)所示的系统称为无零点的二阶系统或典型的二阶系统,而将式(2)所示的系统称为有零点的二阶系统。在不特别声明的情况下,本章讨论的是典型二阶系统的时间响应。 自动控制网www.eadianqi.com版权所有
是二阶系统的特征参数,它们表明二阶系统本身的与外界无关的固有特性。一般将式(1)所示的系统称为无零点的二阶系统或典型的二阶系统,而将式(2)所示的系统称为有零点的二阶系统。在不特别声明的情况下,本章讨论的是典型二阶系统的时间响应。 自动控制网www.eadianqi.com版权所有
二阶系统的特征方程是 本文来自www.eadianqi.com
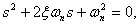 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有
此方程的两个特征根是 本文来自www.eadianqi.com
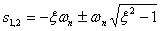 (3)
(3)
本文来自www.eadianqi.com
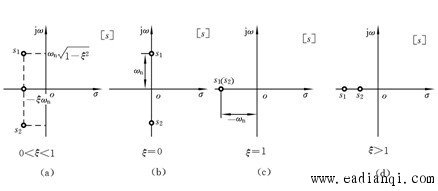
由式(3)可见,随着阻尼比取值的不同,二阶系统的特征根分布不同,亦即二阶系统传递函数的极点分布不同,其分布情况如图(1)所示。不同的极点分布情况,决定了二阶系统在不同的阻尼情况下,其自由响应项不同。由图(1)可知,当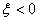 时,即二阶系统出现负阻尼时,其传递函数的两个极点分布在[s]平面的右半平面内,系统不稳定。因此,这里只讨论
时,即二阶系统出现负阻尼时,其传递函数的两个极点分布在[s]平面的右半平面内,系统不稳定。因此,这里只讨论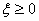 时,二阶系统的响应情况。
时,二阶系统的响应情况。
本文来自www.eadianqi.com
 本文来自www.eadianqi.com
本文来自www.eadianqi.com
图(1) 本文来自www.eadianqi.com
二、二阶系统的单位脉冲响应W(t)和单位阶跃响应
本文来自www.eadianqi.com
在不同阻尼系数下,二阶系统的单位脉冲响应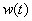 和单位阶跃响应如表1所示。 本文来自www.eadianqi.com
和单位阶跃响应如表1所示。 本文来自www.eadianqi.com
表1 二阶系统的单位脉冲响应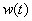 和单位阶跃响应 本文来自www.eadianqi.com
和单位阶跃响应 本文来自www.eadianqi.com
|
阻尼系数 本文来自www.eadianqi.com
|
单位脉冲响应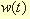 本文来自www.eadianqi.com 本文来自www.eadianqi.com
|
单位阶跃响应 自动控制网www.eadianqi.com版权所有
|
|
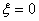
无阻尼 本文来自www.eadianqi.com
|
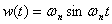 自动控制网www.eadianqi.com版权所有
|
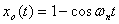 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
|
|
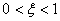
欠阻尼 本文来自www.eadianqi.com
|
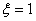 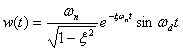 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
|
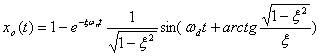 本文来自www.eadianqi.com 本文来自www.eadianqi.com
|
|
临界阻尼 本文来自www.eadianqi.com
|

本文来自www.eadianqi.com
|
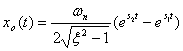 本文来自www.eadianqi.com
|
|
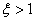
过阻尼 自动控制网www.eadianqi.com版权所有
|
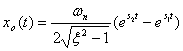 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
|
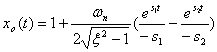 本文来自www.eadianqi.com 本文来自www.eadianqi.com
|
本文来自www.eadianqi.com
其中, ,称
,称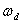 为二阶系统的有阻尼固有频率;
为二阶系统的有阻尼固有频率;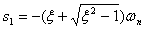 ;
;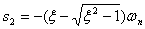 。
。
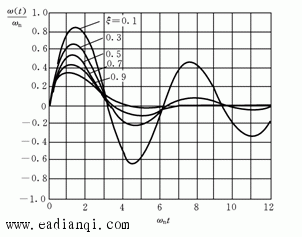
当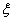 取值不同时,二阶欠阻尼系统的单位脉冲响应曲线如图2所示。由图可知,欠阻尼系统的单位脉冲响应曲线是减幅的正弦振荡曲线,且
取值不同时,二阶欠阻尼系统的单位脉冲响应曲线如图2所示。由图可知,欠阻尼系统的单位脉冲响应曲线是减幅的正弦振荡曲线,且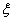 愈小,衰减愈慢,振荡频率
愈小,衰减愈慢,振荡频率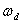 愈大。故欠阻尼系统又称为二阶振荡系统,其幅值衰减的快慢取决于
愈大。故欠阻尼系统又称为二阶振荡系统,其幅值衰减的快慢取决于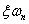 (
( 称为时间衰减常数,记为
称为时间衰减常数,记为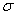 )。
)。
自动控制网www.eadianqi.com版权所有
 本文来自www.eadianqi.com
本文来自www.eadianqi.com
图2
自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有
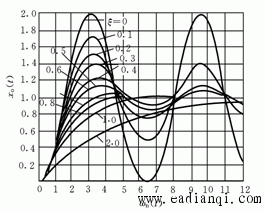
图.3 自动控制网www.eadianqi.com版权所有
当
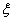
取值不同时,二阶系统的单位阶跃响应如图3所示。由图可知,二阶系统的单位阶跃响应函数的过渡过程随阻尼
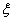
的减小,其振荡特性表现得愈加强烈,当
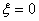
时达到等幅振荡。在
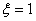
和
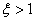
时,二阶系统的过渡过程只具有单调上升的特性,而不会出现振荡。在无振荡单调上升的曲线中,以
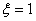
时的过渡过程时间
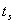
最短。在欠阻尼系统中,当
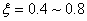
时,不仅其过渡过程时间比
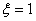
更短,而且振荡也不太严重。因此,一般希望二阶系统工作在
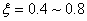
的欠阻尼状态。通过选择合适的特征参数
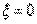
,可以使系统具有合适的过渡过程。
自动控制网www.eadianqi.com版权所有
由于系统输入的不同,二阶系统的单位脉冲响应与单位阶跃响应不同,但是它们随着阻尼比的不同而不同的振荡情况却是一致的。当系统为无阻尼系统时,均为等幅振荡;当系统为欠阻尼系统时,均为减幅振荡;而当系统为临界阻尼或过阻尼系统时,均不会出现振荡。
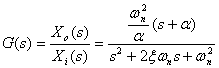 (2)
(2) 本文来自www.eadianqi.com
本文来自www.eadianqi.com 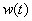 和单位阶跃响应如表1所示。 本文来自www.eadianqi.com
和单位阶跃响应如表1所示。 本文来自www.eadianqi.com 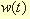
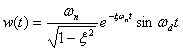
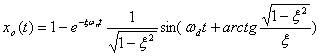
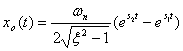 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 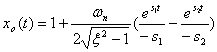 本文来自www.eadianqi.com
本文来自www.eadianqi.com  本文来自www.eadianqi.com
本文来自www.eadianqi.com 