|
1、 由状态空间表达式求传递函数 对于单输入单输出系统,其状态空间表达式为
本文来自www.eadianqi.com
对式(1)求拉普拉斯变换,并设初始条件为零,得到
本文来自www.eadianqi.com
从式(2)可得到
本文来自www.eadianqi.com 式中I为单位矩阵(或称么阵),单位矩阵是主对角线上的元素为1,其余元素全为零的矩阵。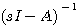 是 是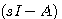 的逆矩阵。将(4)式代入(3)式得到 的逆矩阵。将(4)式代入(3)式得到
自动控制网www.eadianqi.com版权所有
传递函数为
对于有r个输入变量,m个输出变量的多输入多输出线性定常系统,其状态空间表达式为
自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有
A,B,C,D矩阵的元素均为常量。对(7)式和(8)式求取零初始条件下的拉普拉斯变换后可以得到
本文来自www.eadianqi.com G(s)称为传递矩阵,是m*r维矩阵。传递矩阵的每个元素都是单个输出变量与单个输入变量之间的传递函数,即
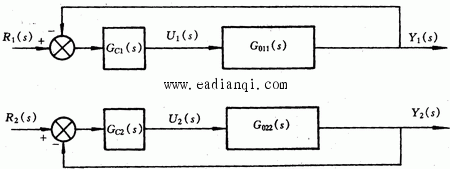
自动控制网www.eadianqi.com版权所有 3、多输入多输出系统的解耦控制式(10)表示的传递函数矩阵说明,在多输入多输出系统中,每一个输入变量对所有输出变量都有影响,而每一个输出变量则与所有的输入变量有关。这种复杂的关联称为变两间的耦合。耦合严重的系统,很难通过改变一个输入信号去影响一个输出信号,造成了控制上的困难。 |图1 是一个有两个输入变量与两个输出变量的交叉的被控对象。可表示为
本文来自www.eadianqi.com 式中
自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com 使得
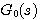 称为一个对角线矩阵,即 称为一个对角线矩阵,即
本文来自www.eadianqi.com
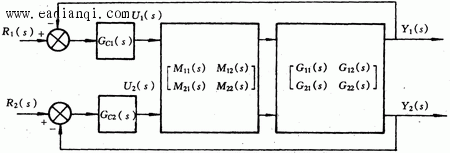
则控制系统可以构成图3所示的控制系统。
式(16)表明,系统已经消除了耦合关系,实现了一个控制器只控制一个输出变量。图4所示的控制系统相当于两个独立的控制回路。这种控制方式称为解耦控制。 |

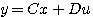 (1)
(1) 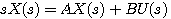 (2)
(2) 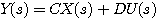 (3)
(3) 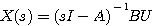 (4)
(4) 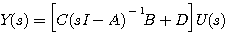 (5)
(5) 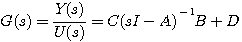 (6) 自动控制网www.eadianqi.com版权所有
(6) 自动控制网www.eadianqi.com版权所有 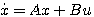 (7)
(7) 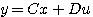 (8)
(8) 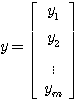
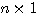 维列向量 本文来自www.eadianqi.com
维列向量 本文来自www.eadianqi.com 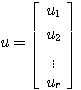
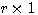 维列向量
维列向量 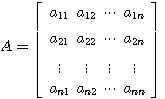
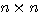 维矩阵
维矩阵 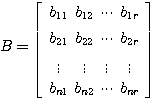
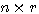 维矩阵 自动控制网www.eadianqi.com版权所有
维矩阵 自动控制网www.eadianqi.com版权所有 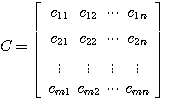
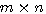 维矩阵
维矩阵 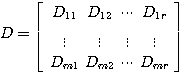
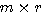 维矩阵
维矩阵 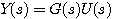 (9) 本文来自www.eadianqi.com
(9) 本文来自www.eadianqi.com 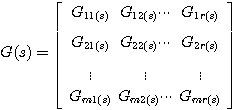 (10)
(10)  (11)
(11) 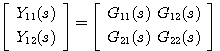
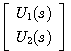 (12) 自动控制网www.eadianqi.com版权所有
(12) 自动控制网www.eadianqi.com版权所有 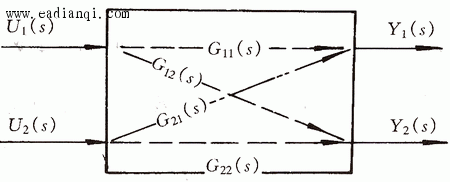
 2耦合被控对象
2耦合被控对象 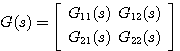 (13)
(13) 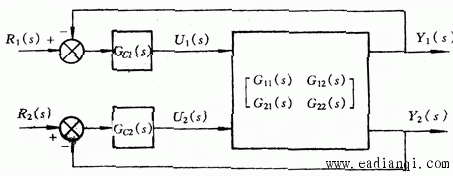
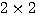 耦合系统结构图 本文来自www.eadianqi.com
耦合系统结构图 本文来自www.eadianqi.com 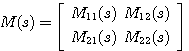 (14)
(14) 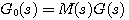
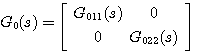 (15)
(15) 
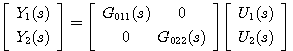 (16)
(16)