|
随着科学技术的发展,被控制的对象越来越复杂,对自动控制的要求也越来越高。面对时变系统,多输入多输出系统、非线性系统等被控量和对控制系统高精度、高性能的严格要求,传统的控制理论已不能适用。同时,计算机技术的发展也要求控制系统地分析,设计中采用计算机技术并在控制系统的组成中使用计算机。因此,适用这些要求的控制系统的另一种数学描述方法----状态空间就应运而生。 2.5.1 状态变量 在对系统动态特性描述中,足以表征系统全部运动状态的最少一组变量,称之为状态变量。只要确定了这组变量在t= 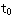 时刻的值以及 时刻的值以及 时的输入函数,则系统在 时的输入函数,则系统在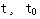 任何时刻的运动状态就会全部确定。状态变量互相间是独立的,但对同一个系统,状态变量的选取并不是唯一的。 任何时刻的运动状态就会全部确定。状态变量互相间是独立的,但对同一个系统,状态变量的选取并不是唯一的。 本文来自www.eadianqi.com 一个用n 阶微分方程描述的系统,有n个独立变量,这n个独立变量就是该系统的状态变量。若用 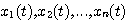 表示这n个状态变量,则可以把这n个状态变量看作是向量x(t)的分量。我们称x(t)为状态变量,它是一个n维向量,记为 表示这n个状态变量,则可以把这n个状态变量看作是向量x(t)的分量。我们称x(t)为状态变量,它是一个n维向量,记为
本文来自www.eadianqi.com
分别以状态变量 本文来自www.eadianqi.com
2.5.2 状态空间表达式1. 状态方程 由系统的状态变量和输入函数构成的一阶微分方程组,称为系统的状态方程。 对于线性系统,可以写成如下形式
本文来自www.eadianqi.com
本文来自www.eadianqi.com
本文来自www.eadianqi.com
若矩阵A和B的元素都是常数,则状态方程是线性定常的。若A和B中有随时间变化的元素,状态方程就是线性时变的。状态方程中不能含有x(t)的高于一阶导数的项和输入函数的导数项。对于非线性系统,状态方程可以写成如下形式
自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
式中f为向量函数。2. 输出方程 描述系统的输出变量与状态变量和输入变量关系的方程,称为输出方程。 线性系统的输出方程具有以下形式
本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有 式中y(t)为m维列向量,称输出向量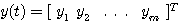 C为m*n维矩阵,称为输出矩阵 C为m*n维矩阵,称为输出矩阵
自动控制网www.eadianqi.com版权所有
线性定常系统的输出矩阵和直接传递矩阵的所有元素均为常量。非线性系统的输出方程可表示为
自动控制网www.eadianqi.com版权所有 式中g称为向量函数。输出方程中不含有变量的任何导数项。 3. 状态空间表达式 系统的状态方程和输出方程总称为系统的状态空间表达式
自动控制网www.eadianqi.com版权所有
图2.35是系统状态空间表达式的结构图。图中用双线箭头表示向量信号。
建立控制系统的状态空间表达式,可以根据系统运动的内在机理直接建立状态方程和输出方程,也可以根据系统的微分方程,传递函数或结构图来建立。后者称为模式转换问题。 1. 由微分方程建立状态空间表达式 (1)不含输入函数倒数项的n阶线性系统。 设n阶线性系统的微分方程具有如下形式
自动控制网www.eadianqi.com版权所有
当 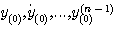 等初始值及在 等初始值及在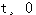 时的输入函数 时的输入函数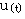 已知时,系统在t时刻的行为就可以完全确定。所以,可以选取 已知时,系统在t时刻的行为就可以完全确定。所以,可以选取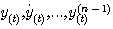 共n个变量为系统的状态变量 共n个变量为系统的状态变量
本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
自动控制网www.eadianqi.com版权所有 方程(2.68)可以写成
自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 式中
自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有
记为
(2)含有输入导数项的n阶线性系统 设n阶线性系统的微分方程具有如下形式
本文来自www.eadianqi.com
对于这种情况,若仍按不含输入导数项的微分方程的处理办法,状态方程就会出现输入函数的导数项,这是不允许的。我们可以这样来选取状态变量
本文来自www.eadianqi.com
本文来自www.eadianqi.com
|
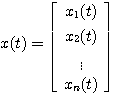
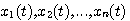 作为坐标而构成的n维空间,称为状态空间。系统在t时刻的状态,就是状态空间的一点。系统在
作为坐标而构成的n维空间,称为状态空间。系统在t时刻的状态,就是状态空间的一点。系统在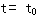 时刻的状态
时刻的状态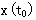 称为初始点,随着时间的变化,x(t)从初始点出发在状态空间描述出一条轨迹,称为状态轨迹。状态魁及表征了系统状态的变化过程。
称为初始点,随着时间的变化,x(t)从初始点出发在状态空间描述出一条轨迹,称为状态轨迹。状态魁及表征了系统状态的变化过程。 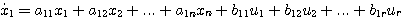
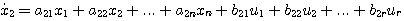 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有  自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 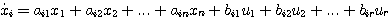 (2.59)
(2.59) 
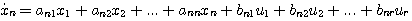
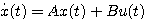 (2.60) 本文来自www.eadianqi.com
(2.60) 本文来自www.eadianqi.com 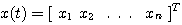
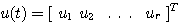 本文来自www.eadianqi.com
本文来自www.eadianqi.com  自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 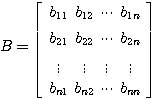
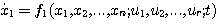
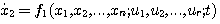 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 
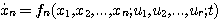 (2.61) 自动控制网www.eadianqi.com版权所有
(2.61) 自动控制网www.eadianqi.com版权所有 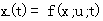 (2.62)
(2.62) 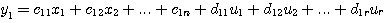 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 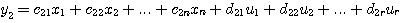
 本文来自www.eadianqi.com
本文来自www.eadianqi.com 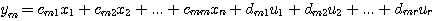 (2.63) 本文来自www.eadianqi.com
(2.63) 本文来自www.eadianqi.com 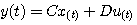 (2.64)
(2.64) 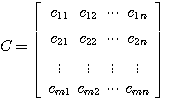
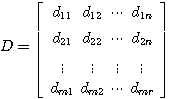
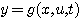 (2.65)
(2.65) 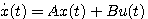
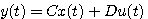 (2.66) 自动控制网www.eadianqi.com版权所有
(2.66) 自动控制网www.eadianqi.com版权所有 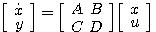 (2.67)
(2.67) 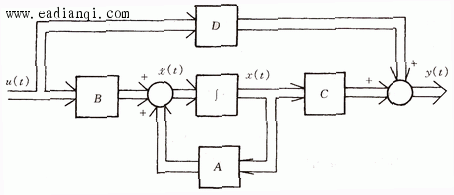
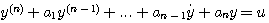 (2.68)
(2.68) 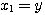
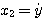
 自动控制网www.eadianqi.com版权所有
自动控制网www.eadianqi.com版权所有 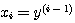
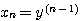
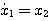
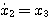
 本文来自www.eadianqi.com
本文来自www.eadianqi.com 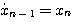
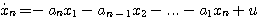
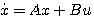 (2.69)
(2.69) 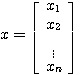
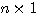 维矩阵
维矩阵 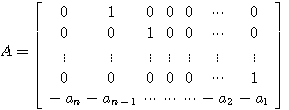
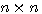 维矩阵 自动控制网www.eadianqi.com版权所有
维矩阵 自动控制网www.eadianqi.com版权所有 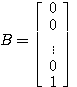
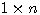 维矩阵 本文来自www.eadianqi.com
维矩阵 本文来自www.eadianqi.com 
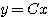
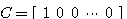
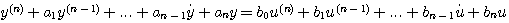 (2.71)
(2.71) 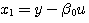

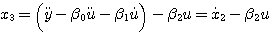 本文来自www.eadianqi.com
本文来自www.eadianqi.com 
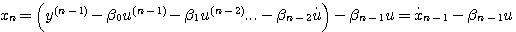
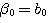 本文来自www.eadianqi.com
本文来自www.eadianqi.com 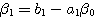 本文来自www.eadianqi.com
本文来自www.eadianqi.com 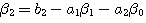
 本文来自www.eadianqi.com
本文来自www.eadianqi.com