在自然科学、社会科学及日常社会生活中,人们广泛地使用各种模型来表示现实事物。模型反映了实物某一方面的属性和特征,是对现实事物的一种表示形式。例如,地球仪是地球的一种模型,军事演习是实战的一种模型,实验室的某些装置是工厂大型设备的模型等。以上这些模型是以实物来表示实物,可以称为具体模型或物理模型。如果对现实事物进行简化、抽象,用方程、公式、图表、曲线等是现实事物的数学模型.数学模型舍弃了现实事物的具体特点而抽象出了它们的共同变化规律.因此,这类模型称为抽象模型. 为了对控制系统进行定性和定量的分析研究,深刻地揭示控制科学的内在规律,建立控制系统的数学模型成为一项必不可少的工作.
控制系统的数学模型主要是指描述控制系统及其各组成部分特性的微分方程、状态空间表达式、差分方程、传递函数、频率特性以及基于神经网络、模糊理论而建立的模型等.
建立控制系统的数学模型有两种基本方法:一种是根据控制系统内部的运动规律,分析各种变量间的因果关系而建立起来的系统的数学模型.这种方法称为机理建模或理论分析法;另一种方法则是根据实际测试的数据或计算数据,按一定的数学方法,归纳出系统的数学模型,这种方法称为系统辨识法或试验分析法.在对控制系统的运动机理、内部规律比较了解的情况下,适合应用机理建模法.用这种方法建立的数学模型,能科学地揭示系统内部及外部的客观规律,因而代表性强,适应面广.在系统运动机理复杂很难掌握其内在规律的情况下,往往需要按系统辨识的方法得到系统的数学模型.这种模型是根据具体对象而得出的,因而适应面较窄,通用性差. 本文来自www.eadianqi.com
建立控制系统的数学模型,是分析研究控制系统的基础.描述各种客观事物内在规律最基本的数学工具就是微分方程.下面,我们通过一些实例,来讨论建立控制系统微分方程的一般过程.
建立控制系统微分方程的主要步骤有:
(1)明确要解决问题的目的和要求,确定系统的输入变量和输出变量.
(2)全面深入细致地分析系统的工作原理、系统内部各变量间的关系.在多数情况下,所研究的系统比较复杂,涉及到的因素很多,不可能把所有复杂的因素都考虑到.因此,必须抓住能代表系统运动规律的主要特征,舍去一些次要因素,对问题进行适当的简化,必要时还必须进行一些合理的假设.
(3)如果把整个控制系统作为一个整体,组成控制系统的各元器件及装置则可以成为子系统。从输入端开始,依照各子系统所遵循的物理定律或其他规律,写出子系统的数学表达式.
(4)消去中间变量,最后得到描述输入变量与输出变量关系的微分方程式。
(5)写出微分方程的规范形式,即所有与输出变量有关的项应在方程左边,所有与输入变量有关的项应在方程右边,所有变量均按降阶排列。
系统微分方程的一般形式是
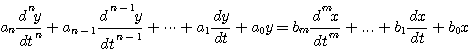 (1) (1)
式中:y为输出变量; 自动控制网www.eadianqi.com版权所有
x为输入变量;
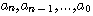 和 和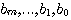 为方程的系数。 为方程的系数。
本书只讨论线性定常系统,因此,这些系数均为常数。
由于控制系统的被控对象和控制元件都具有惯性,当输入量发生变化时,输出量不可能在瞬时完成对输入量的响应,而必须经历一个过渡过程即动态过程,所以我们把描述控制系统的微分方程又称为动态方程。
例1 机械运动系统的数学模型。图1是一个由弹簧、质量块和阻尼器构成的机械运动系统。
弹簧的劲度系数为k(N/m) 质量块的质量为m(Kg) 阻尼器的阻尼系数为f(N·S/m) 阻尼器是吸收系统能量的一种装置,其产生的阻力与活塞运动的速度和阻尼系数成正比。我们现在来建立质量块在外力F(t)作用下位移变化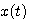 的方程。很显然,这个系统的输入变量为 的方程。很显然,这个系统的输入变量为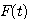 ,输出变量为 ,输出变量为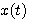 。为了使问题简化,我们忽略质量块重力的影响。 自动控制网www.eadianqi.com版权所有 。为了使问题简化,我们忽略质量块重力的影响。 自动控制网www.eadianqi.com版权所有
作用于质量块的合力P
 (2) 本文来自www.eadianqi.com (2) 本文来自www.eadianqi.com
根据牛顿定律
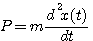 自动控制网www.eadianqi.com版权所有
消去中间变量P,写成规范形式
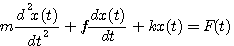 (3) 自动控制网www.eadianqi.com版权所有 (3) 自动控制网www.eadianqi.com版权所有
这个二阶常微分方程就是我们要建立的机械运动系统的数学模型。
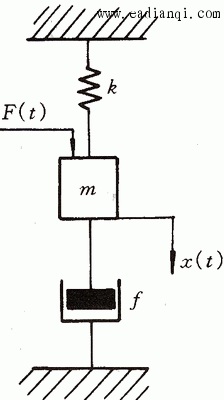
图1 机械运动系统 本文来自www.eadianqi.com
例2 直流电动机的数学模型。直流电动机可以在较宽的速度范围和负载范围内得到连续和准确地控制,因此在控制工程中应用非常广泛。直流电动机产生的力矩与磁通和电枢电流成正比,通过改变电枢电流或改变激磁电流都可以对电流电机的力矩和转速进行控制。图2是一个电枢控制式直流电动机的原理图。在这种控制方式中,激磁电流恒定,控制电压加在电枢上,这是一种普遍采用的控制方式。
设 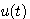 为输入的控制电压 为输入的控制电压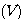
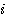 电枢电流 电枢电流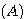 本文来自www.eadianqi.com
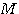 为电机产生的主动力矩 为电机产生的主动力矩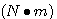
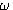 为电机轴的角速度 为电机轴的角速度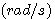
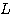 为电机的电感 为电机的电感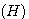
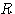 为电枢导数的电阻 为电枢导数的电阻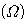 自动控制网www.eadianqi.com版权所有
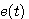 为电枢转动中产生的反电势 为电枢转动中产生的反电势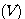
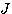 为电机和负载的转动惯量 为电机和负载的转动惯量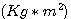
根据电路的克希霍夫定理
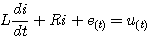 本文来自www.eadianqi.com
电机的主动转矩
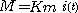 本文来自www.eadianqi.com
其中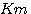 为电机的力矩常数。 为电机的力矩常数。
反电势
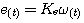 本文来自www.eadianqi.com
式中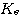 为电机反电势比例系数 为电机反电势比例系数
力矩平衡方程
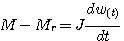 本文来自www.eadianqi.com 本文来自www.eadianqi.com
消去中间变量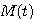 , ,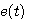 , ,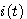 后得到 后得到
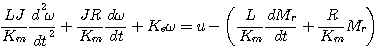 自动控制网www.eadianqi.com版权所有
整理后
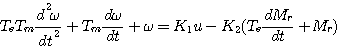 (4) 本文来自www.eadianqi.com (4) 本文来自www.eadianqi.com
式中: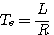 称为直流电动机的电气时间常数; 称为直流电动机的电气时间常数; 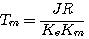 称为直流电动机的机电时间常数; 称为直流电动机的机电时间常数;
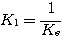 , ,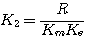 为比例系数。 为比例系数。
直流电动机电枢绕组的电感比较小,一般情况下可以忽略不计,式(4)可简化为
 (5) 本文来自www.eadianqi.com (5) 本文来自www.eadianqi.com
图2直流电动机 自动控制网www.eadianqi.com版权所有
例3 液位系统的数学模型。图3是一个液位系统。
设液箱的横截面积为 .在稳定状态下,流入液箱的水和流出液箱的水流量相同,均为 .在稳定状态下,流入液箱的水和流出液箱的水流量相同,均为 ,此时液箱的水位为 ,此时液箱的水位为 .当流入液箱的流入量有一增量 .当流入液箱的流入量有一增量 时,我们来建立水位增量 时,我们来建立水位增量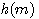 的微分方程。 的微分方程。
液箱水位的变化为
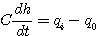 自动控制网www.eadianqi.com版权所有
流出液箱的水的增量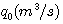 与出口阀的阻力和液箱水位有关。一般情况下, 与出口阀的阻力和液箱水位有关。一般情况下,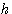 和 和 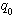 是非线性关系。假设 是非线性关系。假设 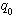 较小,可以近似认为 较小,可以近似认为 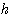 和 和 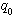 满足线性关系 满足线性关系
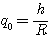 自动控制网www.eadianqi.com版权所有
式中 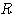 为流出阀的液阻 为流出阀的液阻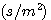 ,是常量。 ,是常量。
消去中间变量 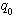 后可得到 后可得到
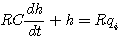 (6) 本文来自www.eadianqi.com (6) 本文来自www.eadianqi.com
若要研究流入量 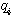 变化对流出量 变化对流出量 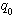 的影响,描述二者关系的微分方程为 的影响,描述二者关系的微分方程为
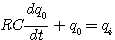 (7) 本文来自www.eadianqi.com (7) 本文来自www.eadianqi.com
这说明,对同一个物理系统,当研究的目的不同时,所得到的数学模型是不一样的。另外,微分方程中的输入变量和输出变量是指系统中具有因果关系的变量,必须和实际系统中具体物质的流入量与输出量区别开来。
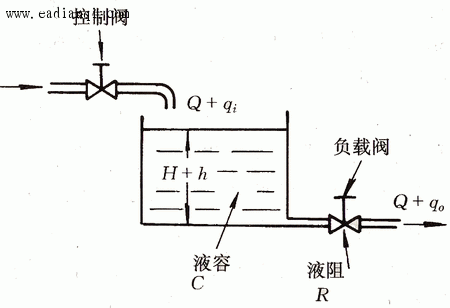
图3 液位系统 本文来自www.eadianqi.com
例4 热力系统的数学模型。图4是一个电加热热水器的示意图。我们现在来建立热水器出口水温受加热器加热量影响的微分方程,为了使问题简化,假设没有热量向周围环境散失,加热器容器中的温度是均匀的,都具有和出口温度相同的温度。设加热器出口水温相对于稳定状态下的增量为 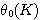 , ,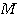 为热水器中水的质量 为热水器中水的质量 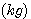 , ,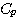 为水的比热容 为水的比热容 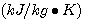 , ,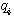 为电加热器传输给水的热流量的增量 为电加热器传输给水的热流量的增量 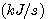 , ,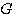 为水的流量 为水的流量 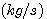 ,根据热量平衡关系 ,根据热量平衡关系
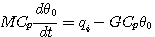 本文来自www.eadianqi.com 本文来自www.eadianqi.com
整理后为
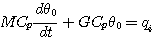 (8) 本文来自www.eadianqi.com (8) 本文来自www.eadianqi.com
若要考虑水入口温度的影响,设入口水温的变化量为 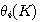 ,则有 ,则有
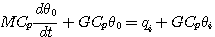 (9) 自动控制网www.eadianqi.com版权所有 (9) 自动控制网www.eadianqi.com版权所有
若要考虑更多的因素,微分方程将变得更加复杂。
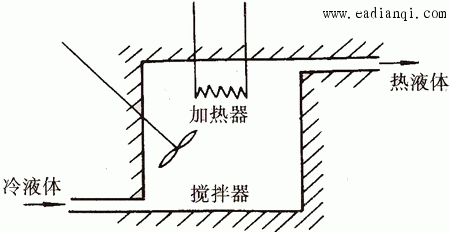
图4 电热水器 自动控制网www.eadianqi.com版权所有
由此可以看出合理假设和简化在建立系统的数学模型中是很重要的。不同的简化和假设会得到不同的模型。假设的条件太多,过分简化,虽然数学模型简单,数学处理容易,但可能无法反映出事物的主要特征或达不到应有的准确性。若考虑的因素太多,数学模型将变得很复杂,数学处理困难,增加了解决问题的难度,有时甚至会出现次要因素掩盖了事物主要特征的现象,得不出正确的结果。假设、简化到什么程度,并无统一的规定,主要根据具体问题和实际经验来决定。
系统的微分方程建立以后,还必须对其进行验证。要把根据数学模型进行理论分析的结果和实际结果或实验结果相比较,证明数学模型的合理性。若不符合要求,则必须进行修改。一个成熟的数学模型往往要经过多次修改和验证才能确定下来。
建立数学模型是一个培养综合应用各种知识,不断创造新的过程。建立数学模型需要有综合分析和抓住问题本质的能力,需要有较高的抽象概括能力和较高的数学素养,也需要有科学的思维方法。数学模型不仅仅用来解释已发生的现象,更重要的是要预测事物的发展,为未来的决策提供指南。因此,建立数学模型的过程也是新观点、新方法产生的过程,是一种不断创新的过程。培养创新的意识、创新的能力,和掌握科学知识是同等重要的。
|
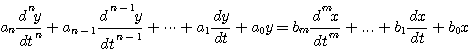 (1)
(1)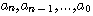 和
和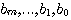 为方程的系数。
为方程的系数。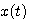 的方程。很显然,这个系统的输入变量为
的方程。很显然,这个系统的输入变量为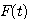 ,输出变量为
,输出变量为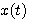 。为了使问题简化,我们忽略质量块重力的影响。
。为了使问题简化,我们忽略质量块重力的影响。  (2)
(2) 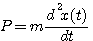
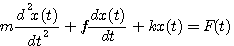 (3)
(3) 
 为输入的控制电压
为输入的控制电压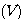
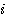 电枢电流
电枢电流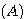
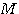 为电机产生的主动力矩
为电机产生的主动力矩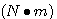
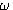 为电机轴的角速度
为电机轴的角速度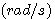
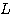 为电机的电感
为电机的电感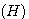
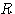 为电枢导数的电阻
为电枢导数的电阻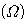
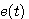 为电枢转动中产生的反电势
为电枢转动中产生的反电势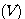
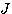 为电机和负载的转动惯量
为电机和负载的转动惯量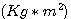
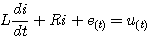
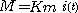
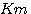 为电机的力矩常数。
为电机的力矩常数。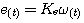
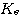 为电机反电势比例系数
为电机反电势比例系数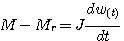 本文来自www.eadianqi.com
本文来自www.eadianqi.com 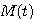 ,
,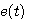 ,
,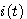 后得到
后得到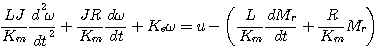
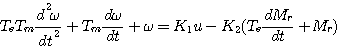 (4) 本文来自www.eadianqi.com
(4) 本文来自www.eadianqi.com 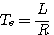 称为直流电动机的电气时间常数;
称为直流电动机的电气时间常数; 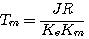 称为直流电动机的机电时间常数;
称为直流电动机的机电时间常数;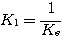 ,
,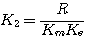 为比例系数。
为比例系数。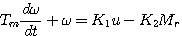 (5)
(5) 
 .在稳定状态下,流入液箱的水和流出液箱的水流量相同,均为
.在稳定状态下,流入液箱的水和流出液箱的水流量相同,均为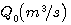 ,此时液箱的水位为
,此时液箱的水位为 .当流入液箱的流入量有一增量
.当流入液箱的流入量有一增量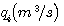 时,我们来建立水位增量
时,我们来建立水位增量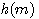 的微分方程。
的微分方程。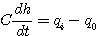
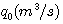 与出口阀的阻力和液箱水位有关。一般情况下,
与出口阀的阻力和液箱水位有关。一般情况下,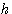 和
和 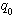 是非线性关系。假设
是非线性关系。假设 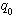 较小,可以近似认为
较小,可以近似认为 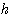 和
和 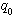 满足线性关系
满足线性关系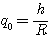
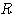 为流出阀的液阻
为流出阀的液阻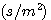 ,是常量。
,是常量。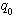 后可得到
后可得到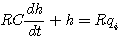 (6)
(6) 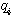 变化对流出量
变化对流出量 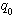 的影响,描述二者关系的微分方程为
的影响,描述二者关系的微分方程为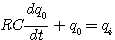 (7)
(7) 
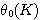 ,
,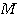 为热水器中水的质量
为热水器中水的质量 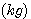 ,
,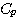 为水的比热容
为水的比热容 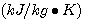 ,
,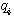 为电加热器传输给水的热流量的增量
为电加热器传输给水的热流量的增量 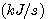 ,
,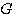 为水的流量
为水的流量  ,根据热量平衡关系
,根据热量平衡关系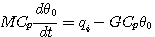 本文来自www.eadianqi.com
本文来自www.eadianqi.com 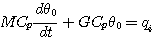 (8)
(8) 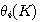 ,则有
,则有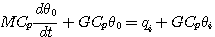 (9)
(9) 