|
□ 闭环调速系统各环节动态数学模型 □ 系统的数学模型和传递函数 □ 闭环调速系统稳定性分析 |
 |
|
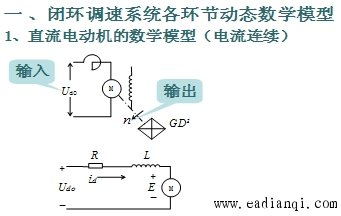
设R、L为常数、忽略电枢反应、Φ不变、GD2(轴上惯量均匀)常数,直流电机可以等效为左下图。 ①电枢回路传函 在电流连续的条件下,直流电动机的电枢回路电压平衡方程为 |
|
|
|
其中,Tl=L/R 为电磁时间常数 自动控制网www.eadianqi.com版权所有 进行拉氏变换得 |
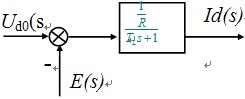
| 得电压与电流之间的传递函数 |
|
|
 |
|
②电动机传动系统传函 电动机轴上的转矩和转速服从电力拖动系统的运动方程式 |
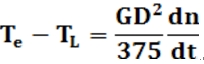 |
|
|
|
|
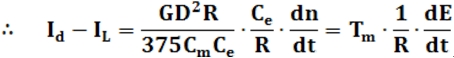 |
| 对上式两端取拉氏变换得 |
|
|
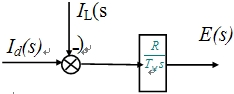 |
|
将上面两环节输入输出量连接起来。并考虑 |
| 即可得到额定励磁下他励直流电动机动态结构图 |
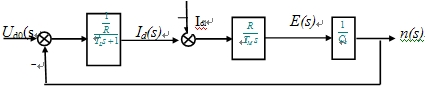 |
| 干扰量的综合点前移,化简得: |
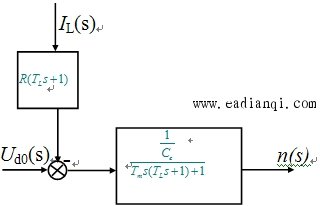 |
| 直流电动机在电流连续时电压与转速间的传函(IL=0): |
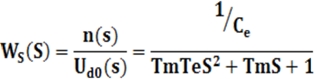 |
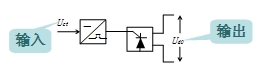
| 2、触发器和晶闸管整流装置数学模型 |
 |
|
① 稳态:Udo=KsUct 自动控制网www.eadianqi.com版权所有 ② 动态: 滞后环节 晶闸管触发导通后,在尚未关断之前,虽然改变了控制电压Uct 的值,但整流电压的瞬时波形和 角并不能立即跟随Uct的变化,通常把这个滞后时间称作整流装置的失控时间,用Ts来表示。 最大失控时间为两个相邻自然换相点之间的时间,即 |
|
|
|
相对于整个系统的时间响应来说,Ts 是不大的。通常可用简单算术平均值,即Ts =Tsmax/2 ,Ts不同整流电路 取值不同。 ③ 晶闸管触发器和整流装置可以看成是一个具有纯滞后的放大环节,其输入输出关系为 |
|
|
| 应用拉氏位移定理,其传递函数为 |
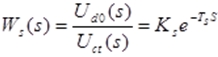 |
| 将按泰勒级数展开,则上式变成 |
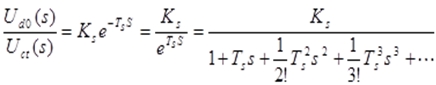 |
| 由于很小,可忽略高次项,可将晶闸管变流装置近似成一阶惯性环节来处理,其传函为 |
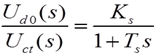 |
| 晶闸管触发器和整流装置动态结构图为: |
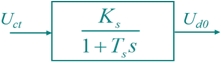 |
| 3、比例放大器传函(输出响应可认为是瞬时变化的) |
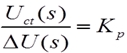 (响应时瞬时的) (响应时瞬时的) |
| 4、测速发电机传函(输出响应可认为是瞬时变化的) |
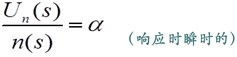 |
|
二、系统的数学模型和传递函数 自动控制网www.eadianqi.com版权所有 将上述四个环节按系统中的相互关系连接在一起,便得到单闭环调速系统动态结构图。 |
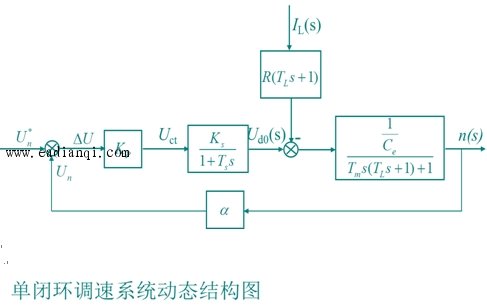 |
| 当不考虑负载,即 IL=0 时,系统开环传函为 |
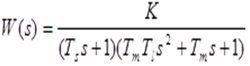 |
| 令IL=0 得闭环系统传函为: |
 |
|
其中,K=KpKsα/Ce 三、闭环调速系统稳定性分析 系统闭环传函特征方程为 |
|
|
|
◎稳定条件 本文来自www.eadianqi.com 根据反馈控制闭环调速系统的特征方程和劳斯--古尔维茨判据,可以推导出其稳定条件为 |
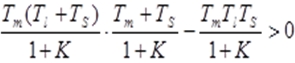 |
|
或 |
可得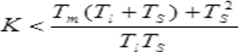 |
即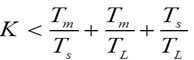 |
| 上式表明:在系统参数Tm、TL、Ts 确定的前提下,从动态稳定性考虑,闭环系统的开环放大系数K必须满足上式,K 超过此值,系统将不稳定。按静态调速指标确定的K值还必须按动态稳定性进行验算。当二者发生矛盾时,还要采取动态校正措施加以改造。 |