|
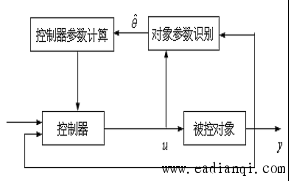
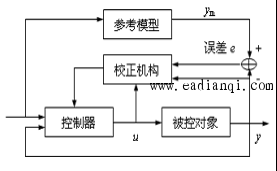
(一)线性系统理论 线性系统理论是现代控制理论中最基本的组成部分,也是比较成熟的部分。要分析系统的特性,首先要建立系统的数学模型。经典控制理论中用微分方程、传递函数和频率特性来描述,而这里用状态方程来描述。状态方程不但描述了系统的输入输出关系,而且描述了系统内部一些状态变量的随时间变化关系。 (二)系统辨识 这是现代控制理论中一个很活跃的分支。 所谓系统辨识,就是通过观测一个系统或一个过程的输入、输出关系来确定其数学模型的方法。系统辨识理论不但广泛应用于工业、国防、农业和交通等工程控制系统中,而且还应用于计量经济学、社会学、生理学、生物医学和生态学等领域。 如对于人—机器—环境系统中人的性能、瞳孔和肌肉的控制功能、新陈代谢以及脑电波等,已经获得了很成功的模型。 (三)最优控制 最优控制是现代控制理论中一个重要的组成部分。最优控制问题是在已知系统的状态方程、初始条件以及某些约束条件下,寻求一个最优控制向量,使系统的状态或输出在控制向量作用下满足某种最佳准则或使某一指标泛函达到最优值。 本文来自www.eadianqi.com (四)最优估计 最优估计也是现代控制理论的一个很重要分支。在通信工程中,接收到的信号总是由有用信号和干扰噪声混合组成的。 y(t)=S(t)+n(t) 希望从接收信号y(t)中分离出有用信号S(t),就要用到最优估计,即由y(t)求S(t)的估计验后数据处理也要用到最优估计。 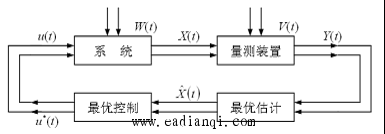 图1 最优估计与最优控制框图 (五)自适应控制 自适应控制也是现代控制理论中近年来发展比较快的一个活跃的分支。 自适应控制一般分为两大类: 一类称为模型参考自适应控制(Model Reference Adaptive Control); 另一类称为自校正自适应应控制(Self-Turning Adaptive Control)。 |