|
频率法中对系统稳定性的分析是应用奈奎斯特(Nyquist)判据进行的。奈奎斯特判据 是根据控制系统的开环频率特性判断闭环系统是否稳定的判据。应用奈奎斯特判据,不仅能解决系统是否稳定的问题,而且还能了解系统稳定的程度,并找出改善系统动态特性的途径。因此,奈奎斯特判据是频域分析的基础。
4.5.1映射定理
设F(s)是一个单值解析的复变函数。对于s平面上一条不通过任何奇点的封闭曲线C,在F(s)平面上必有一条封闭的曲线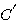 与之对应,该封闭曲线 与之对应,该封闭曲线 是曲线C的映射。如果s平面上的封闭曲线C 内部包含了F(s)的P 个极点和Z 个零点,且动点s 是沿顺时针方向在封闭曲线上变化的,则在F(s)平面上相应的封闭曲线 包围坐标原点的周数和方向可以表示为 自动控制网www.eadianqi.com版权所有 是曲线C的映射。如果s平面上的封闭曲线C 内部包含了F(s)的P 个极点和Z 个零点,且动点s 是沿顺时针方向在封闭曲线上变化的,则在F(s)平面上相应的封闭曲线 包围坐标原点的周数和方向可以表示为 自动控制网www.eadianqi.com版权所有
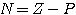 (4.40) 自动控制网www.eadianqi.com版权所有 (4.40) 自动控制网www.eadianqi.com版权所有
式中N 是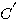 包围原点的周数,若N>0,则表示 包围原点的周数,若N>0,则表示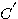 顺时针包围F(s) 平面的原点,若N<0 ,则 顺时针包围F(s) 平面的原点,若N<0 ,则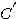 逆时针包围F(s)平面的原点,若N=0,则 逆时针包围F(s)平面的原点,若N=0,则 不包围F(s)平面的原点。这里不对映射原理进行证明。对此有兴趣的读者可以参阅其他有关书籍。 不包围F(s)平面的原点。这里不对映射原理进行证明。对此有兴趣的读者可以参阅其他有关书籍。 本文来自www.eadianqi.com
4.5.2 奈奎斯特判据
映射原理为判断控制系统的稳定性提供了依据。设 本文来自www.eadianqi.com
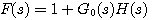 (4.41) 自动控制网www.eadianqi.com版权所有 (4.41) 自动控制网www.eadianqi.com版权所有
根据控制系统的稳定的充分必要条件,若系统稳定,则s 平面右半边没有闭环极点,既没有特征方程的根。 特征方程的根就是函数F(s)的 零点。F(s)的极点则与开环传递函数的极点相同。若F(s)曲线是已知封闭曲线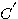 ,则可以确定F(s)包围原点的周数及包围原点的的方向.又因为F(s)与开环传递函数的极点相同,所以可以根据开环传递函数确定s平面上封闭曲线C所包含的F(s)极点数P。按照映射原理,s平面上的封闭曲线C所包含的F(s)的零点数即可确定。问题的关键是在s平面上找到一条能包围整个s平面的右半边的封闭曲线。这条曲线就是奈奎斯特轨迹。 本文来自www.eadianqi.com ,则可以确定F(s)包围原点的周数及包围原点的的方向.又因为F(s)与开环传递函数的极点相同,所以可以根据开环传递函数确定s平面上封闭曲线C所包含的F(s)极点数P。按照映射原理,s平面上的封闭曲线C所包含的F(s)的零点数即可确定。问题的关键是在s平面上找到一条能包围整个s平面的右半边的封闭曲线。这条曲线就是奈奎斯特轨迹。 本文来自www.eadianqi.com
1. 奈奎斯特轨迹
奈奎斯特轨迹是由整个虚轴和位于s平面右半边的半径为无穷大的半圆构成的封闭曲线,动点s在曲线上顺时针方向移动。图4.20时奈奎斯特轨迹的示意图。奈奎斯特轨迹不能通过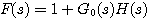 的任何零点和极点。 的任何零点和极点。 本文来自www.eadianqi.com
奈奎斯特轨迹是s 平面上的一条封闭曲线,而与之对应的函数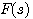 在 在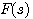 复平面上是一条什么样的封闭曲线呢?我们把奈奎斯特轨迹划分为两部分:一部分是半径为无穷大的半圆;另一部分是整个虚轴。现在来分析这两部分在 复平面上是一条什么样的封闭曲线呢?我们把奈奎斯特轨迹划分为两部分:一部分是半径为无穷大的半圆;另一部分是整个虚轴。现在来分析这两部分在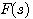 平面上的映射。 本文来自www.eadianqi.com 平面上的映射。 本文来自www.eadianqi.com
当s趋近于无穷大时,由于开环传递函数分母的阶次n一般都大于分子的阶次m,所以有 本文来自www.eadianqi.com
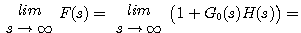 常量 常量 本文来自www.eadianqi.com
若n>m,则上面的常量为1,若n=m,则为其他常量。总之,s平面上奈奎斯特轨迹的无穷大半圆在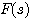 平面上的映射是实轴上的一个点。 平面上的映射是实轴上的一个点。 本文来自www.eadianqi.com
当动点s在奈奎斯特轨迹上的另一部分,即整个虚轴上由负无穷大向无穷大变化时,由于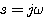 ,所以有 本文来自www.eadianqi.com ,所以有 本文来自www.eadianqi.com
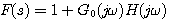 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
其中的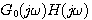 正是开环频率特性。所以,可以说奈奎斯特轨迹在 正是开环频率特性。所以,可以说奈奎斯特轨迹在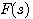 的映射就是开环频率特性。 的映射就是开环频率特性。 本文来自www.eadianqi.com
若已知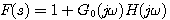 包围 包围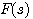 平面原点的周数及方向N,又知道奈奎斯特轨迹所包围的开环传递函数的极点数P,则位于s平面右半边特征方程的根的个数Z即可根据映射定理计算出来,系统的稳定性也随之确定了。 本文来自www.eadianqi.com 平面原点的周数及方向N,又知道奈奎斯特轨迹所包围的开环传递函数的极点数P,则位于s平面右半边特征方程的根的个数Z即可根据映射定理计算出来,系统的稳定性也随之确定了。 本文来自www.eadianqi.com
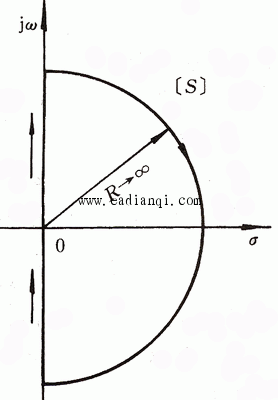
图 4.20 奈奎斯特轨迹 自动控制网www.eadianqi.com版权所有
函数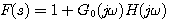 构成的复平面与开环频率特性 构成的复平面与开环频率特性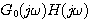 构成的复平面,实轴坐标仅差1. 构成的复平面,实轴坐标仅差1.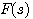 平面上封闭曲线对原点的包围就是 平面上封闭曲线对原点的包围就是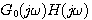 平面上对 平面上对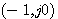 点的包围。为了简便,在我们绘制出开环频率特性以后,不必再转为 点的包围。为了简便,在我们绘制出开环频率特性以后,不必再转为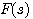 函数,直接使用开环频率特性判断系统是否稳定就可以了。 函数,直接使用开环频率特性判断系统是否稳定就可以了。 自动控制网www.eadianqi.com版权所有
当开环传递函数含有积分环节时,例如 本文来自www.eadianqi.com
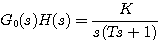 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有

图 4.21 有积分环节情况下的奈奎斯特轨迹 本文来自www.eadianqi.com
有一个s=0的极点,这个极点正好位于奈奎斯特轨迹上,违反了封闭曲线C 不能有奇点的规定。为了解决这个问题,我们用一个半径为无穷小的半圆从右面绕过原点,如图4.21 所示。这样,除了原点之外奈奎斯特轨迹仍然包围s平面右半边,无穷小半原在开环频率特性的复平面上,即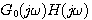 平面上的映射唯一无穷大圆弧段。 本文来自www.eadianqi.com 平面上的映射唯一无穷大圆弧段。 本文来自www.eadianqi.com
2. 奈奎斯特判据
奈奎斯特判据是对奈奎斯特轨迹应用映射原理的结果。 本文来自www.eadianqi.com
奈奎斯特判据:
设开环传递函数位于s平面右半边的极点个数为P。若P=0,闭环系统稳定的充分必要条件是当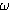 从负无穷大连续变化到正无穷大时, 从负无穷大连续变化到正无穷大时,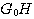 平面上的开环频率特性曲线不包围 平面上的开环频率特性曲线不包围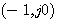 点,否则系统不稳定。若 点,否则系统不稳定。若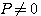 ,闭环系统稳定的充分必要条件是当 ,闭环系统稳定的充分必要条件是当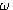 从负无穷大变化到正无穷大时, 从负无穷大变化到正无穷大时,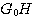 平面上的开环频率特性曲线逆时针方向包围 平面上的开环频率特性曲线逆时针方向包围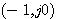 点P周。 自动控制网www.eadianqi.com版权所有 点P周。 自动控制网www.eadianqi.com版权所有
例4 控制系统的开环传递函数为 自动控制网www.eadianqi.com版权所有
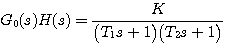 自动控制网www.eadianqi.com版权所有
判断该系统的稳定性。
解 该系统的开环频率特性如图4.22所示。 本文来自www.eadianqi.com
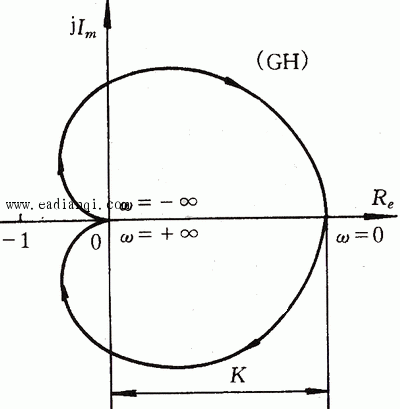
图 4.22 控制系统的开环频率特性 自动控制网www.eadianqi.com版权所有
开环传递函数在s平面右半边无极点,即P=0,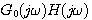 曲线不包围 曲线不包围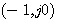 点,所以系统稳定。 本文来自www.eadianqi.com 点,所以系统稳定。 本文来自www.eadianqi.com
例5 控制系统的开环传递函数为 本文来自www.eadianqi.com
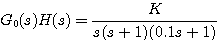 本文来自www.eadianqi.com
判断当K=2和K=20时系统的稳定性。
解 当K=2时,绘出系统的开环频率特性如图4.23所示。
当K=20时,绘出系统的开环频率特性如图4.24所示。 自动控制网www.eadianqi.com版权所有
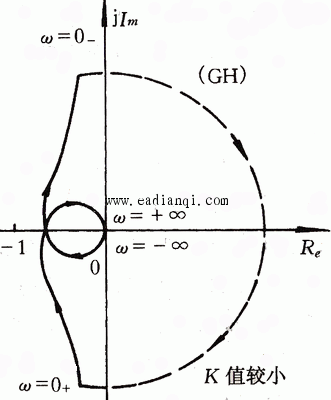
图 4.23 K=2时的开环频率特性
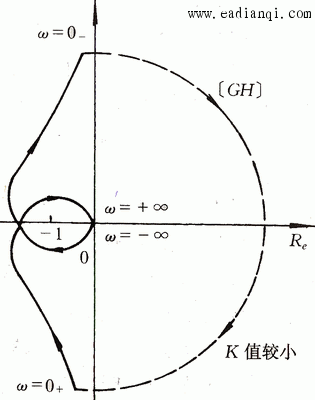
图4.24 K=20时的开环频律特性 自动控制网www.eadianqi.com版权所有
由于开环传递函数中含有积分环节,所以奈奎斯特轨迹在原点处增加了无穷小半圆。 本文来自www.eadianqi.com
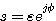 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
s从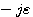 从原点右侧绕到 从原点右侧绕到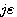 ,当 ,当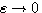 时,该无穷小半圆在开环频率特性上是无穷大半圆弧,如图中虚线所示。 自动控制网www.eadianqi.com版权所有 时,该无穷小半圆在开环频率特性上是无穷大半圆弧,如图中虚线所示。 自动控制网www.eadianqi.com版权所有
图4.23的开环频率特性不包围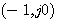 点,而本例中P=0,所以系统稳定。求解特征方程,可得到特征方程的根为 点,而本例中P=0,所以系统稳定。求解特征方程,可得到特征方程的根为 自动控制网www.eadianqi.com版权所有
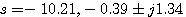 本文来自www.eadianqi.com 本文来自www.eadianqi.com
特征根均具有负实部,和应用奈奎斯特判据的结论完全一致。 自动控制网www.eadianqi.com版权所有
图4.24的开环频率特性包围了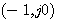 点(顺时针方向,2周)而P=0,根据奈奎斯特判据,系统是不稳定的。求解特征方程可得 点(顺时针方向,2周)而P=0,根据奈奎斯特判据,系统是不稳定的。求解特征方程可得 自动控制网www.eadianqi.com版权所有
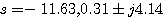 自动控制网www.eadianqi.com版权所有 自动控制网www.eadianqi.com版权所有
特征方程的共轭负数根具有正实部,从而验证了奈奎斯特判据。
例6 系统的开环传递函数为 本文来自www.eadianqi.com
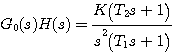 本文来自www.eadianqi.com 本文来自www.eadianqi.com
判断系统的稳定性。
解 系统的稳定性与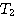 和 和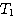 的取值有关。不同情况下的开环频率特性如图4.25所示。 自动控制网www.eadianqi.com版权所有 的取值有关。不同情况下的开环频率特性如图4.25所示。 自动控制网www.eadianqi.com版权所有

图 4.25 T值不同情况下的开环频律特性 本文来自www.eadianqi.com
本例中P=0,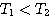 时,开环频率特性不包围 时,开环频率特性不包围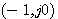 点,系统稳定。 点,系统稳定。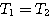 时,开环频率特性正好通过 时,开环频率特性正好通过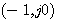 点,说明系统处于临界稳定状态,闭环极点位于虚轴上。 点,说明系统处于临界稳定状态,闭环极点位于虚轴上。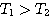 时,开环频率特性顺时针方向包围 时,开环频率特性顺时针方向包围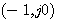 点两周,系统不稳定。 自动控制网www.eadianqi.com版权所有 点两周,系统不稳定。 自动控制网www.eadianqi.com版权所有
例7 已知控制系统的开环传递函数为 自动控制网www.eadianqi.com版权所有
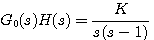 本文来自www.eadianqi.com 本文来自www.eadianqi.com
判断闭环系统的稳定性。 自动控制网www.eadianqi.com版权所有
解 该系统的开环频率特性如图4.26所示。
本例中有一个开环极点s=1位于s平面右半边,P=1,而开环频率特性顺时针包围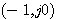 点一周,根据奈奎斯特判据,此系统稳定。 本文来自www.eadianqi.com 点一周,根据奈奎斯特判据,此系统稳定。 本文来自www.eadianqi.com
判断开环频率特性包围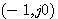 点的方法是假设一个起点在 点的方法是假设一个起点在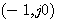 点。矢端在开环频率特性曲线上的矢量。当 点。矢端在开环频率特性曲线上的矢量。当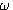 从 从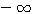 变化到 变化到 时,该矢量的副角变化量与 时,该矢量的副角变化量与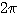 之比即为包围 之比即为包围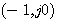 点的周数。 点的周数。 自动控制网www.eadianqi.com版权所有
若开环频率特性顺时针包围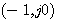 点,系统总是不稳定的。 点,系统总是不稳定的。 自动控制网www.eadianqi.com版权所有
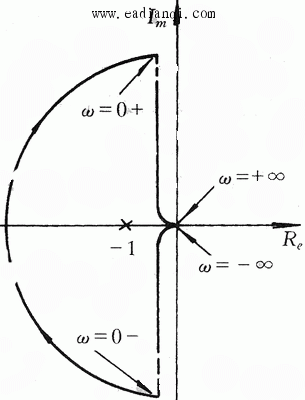
图 4.26 例7的开环频律特性 本文来自www.eadianqi.com
3。 用对数频率特性分析系统的稳定性。
系统开环频率特性的极坐标图与开环对数频率图有如下关系 本文来自www.eadianqi.com
在极坐标图上,以原点为圆心的单位圆,因其模为1,对应于对数幅频特性的零分贝点,其相角均为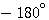 .所以负实轴对应于对数相频特性的 .所以负实轴对应于对数相频特性的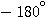 线。 自动控制网www.eadianqi.com版权所有 线。 自动控制网www.eadianqi.com版权所有
对于开环传递函数在s平面右半边无极点的系统(称为开环稳定),若系统开环对数副频特性在穿越0dB线时,所对应的对数相频特性曲线的相位角大于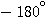 (绝对值大于180),则闭环系统稳定,否则不稳定。 本文来自www.eadianqi.com (绝对值大于180),则闭环系统稳定,否则不稳定。 本文来自www.eadianqi.com
4.5.3 相对稳定性
只判断控制系统是否稳定,以稳定和不稳定来区分系统,这种稳定的分析称为绝对稳定分析问题。在更多的情况下,我们还想知道系统的稳定程度如何。只就是相对稳定问题。应用奈奎斯特判据不仅可以判断系统是否稳定,而且可以解决相对稳定性问题。 自动控制网www.eadianqi.com版权所有
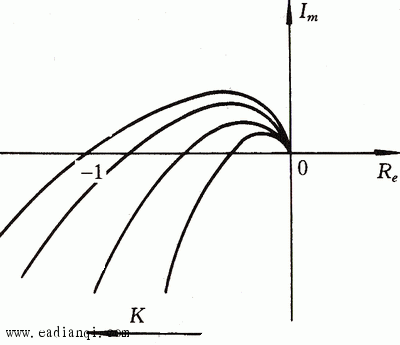
图4.27是一个控制系统的开环频率特性的局部(P=0).当系统的K较小时,开环频率特性曲线不包围 点。继续增大K,开环频率特性曲线仍未包围 点。继续增大K,开环频率特性曲线仍未包围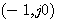 ,系统还是稳定的。但开环频率特性曲线更靠近 ,系统还是稳定的。但开环频率特性曲线更靠近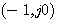 点。我们说它的稳定程度不如前者。再增大K,开环频率特性曲线通过 点。我们说它的稳定程度不如前者。再增大K,开环频率特性曲线通过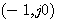 点,系统处于临界稳定状态。随着K的继续增大,开环频率特性曲线包围了 点,系统处于临界稳定状态。随着K的继续增大,开环频率特性曲线包围了 点,系统变成了不稳定系统。图4.27 表明,对于稳定的系统,开环频率特性曲线越靠近 点,系统变成了不稳定系统。图4.27 表明,对于稳定的系统,开环频率特性曲线越靠近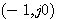 点,系统的稳定程度越低。对于不稳定的系统,开环频率特性曲线离 点,系统的稳定程度越低。对于不稳定的系统,开环频率特性曲线离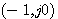 点越远,不稳定程度越大。 点越远,不稳定程度越大。 自动控制网www.eadianqi.com版权所有
|
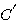 与之对应,该封闭曲线
与之对应,该封闭曲线 是曲线C的映射。如果s平面上的封闭曲线C 内部包含了F(s)的P 个极点和Z 个零点,且动点s 是沿顺时针方向在封闭曲线上变化的,则在F(s)平面上相应的封闭曲线 包围坐标原点的周数和方向可以表示为 自动控制网www.eadianqi.com版权所有
是曲线C的映射。如果s平面上的封闭曲线C 内部包含了F(s)的P 个极点和Z 个零点,且动点s 是沿顺时针方向在封闭曲线上变化的,则在F(s)平面上相应的封闭曲线 包围坐标原点的周数和方向可以表示为 自动控制网www.eadianqi.com版权所有 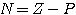 (4.40) 自动控制网www.eadianqi.com版权所有
(4.40) 自动控制网www.eadianqi.com版权所有 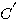 包围原点的周数,若N>0,则表示
包围原点的周数,若N>0,则表示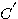 顺时针包围F(s) 平面的原点,若N<0 ,则
顺时针包围F(s) 平面的原点,若N<0 ,则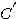 逆时针包围F(s)平面的原点,若N=0,则
逆时针包围F(s)平面的原点,若N=0,则 不包围F(s)平面的原点。这里不对映射原理进行证明。对此有兴趣的读者可以参阅其他有关书籍。
不包围F(s)平面的原点。这里不对映射原理进行证明。对此有兴趣的读者可以参阅其他有关书籍。 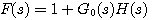 (4.41) 自动控制网www.eadianqi.com版权所有
(4.41) 自动控制网www.eadianqi.com版权所有 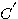 ,则可以确定F(s)包围原点的周数及包围原点的的方向.又因为F(s)与开环传递函数的极点相同,所以可以根据开环传递函数确定s平面上封闭曲线C所包含的F(s)极点数P。按照映射原理,s平面上的封闭曲线C所包含的F(s)的零点数即可确定。问题的关键是在s平面上找到一条能包围整个s平面的右半边的封闭曲线。这条曲线就是奈奎斯特轨迹。 本文来自www.eadianqi.com
,则可以确定F(s)包围原点的周数及包围原点的的方向.又因为F(s)与开环传递函数的极点相同,所以可以根据开环传递函数确定s平面上封闭曲线C所包含的F(s)极点数P。按照映射原理,s平面上的封闭曲线C所包含的F(s)的零点数即可确定。问题的关键是在s平面上找到一条能包围整个s平面的右半边的封闭曲线。这条曲线就是奈奎斯特轨迹。 本文来自www.eadianqi.com 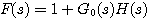 的任何零点和极点。
的任何零点和极点。 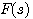 在
在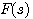 复平面上是一条什么样的封闭曲线呢?我们把奈奎斯特轨迹划分为两部分:一部分是半径为无穷大的半圆;另一部分是整个虚轴。现在来分析这两部分在
复平面上是一条什么样的封闭曲线呢?我们把奈奎斯特轨迹划分为两部分:一部分是半径为无穷大的半圆;另一部分是整个虚轴。现在来分析这两部分在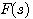 平面上的映射。
平面上的映射。 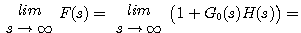 常量
常量 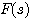 平面上的映射是实轴上的一个点。
平面上的映射是实轴上的一个点。 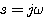 ,所以有
,所以有 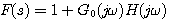
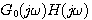 正是开环频率特性。所以,可以说奈奎斯特轨迹在
正是开环频率特性。所以,可以说奈奎斯特轨迹在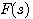 的映射就是开环频率特性。
的映射就是开环频率特性。 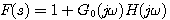 包围
包围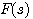 平面原点的周数及方向N,又知道奈奎斯特轨迹所包围的开环传递函数的极点数P,则位于s平面右半边特征方程的根的个数Z即可根据映射定理计算出来,系统的稳定性也随之确定了。
平面原点的周数及方向N,又知道奈奎斯特轨迹所包围的开环传递函数的极点数P,则位于s平面右半边特征方程的根的个数Z即可根据映射定理计算出来,系统的稳定性也随之确定了。 
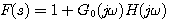 构成的复平面与开环频率特性
构成的复平面与开环频率特性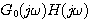 构成的复平面,实轴坐标仅差1.
构成的复平面,实轴坐标仅差1.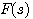 平面上封闭曲线对原点的包围就是
平面上封闭曲线对原点的包围就是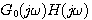 平面上对
平面上对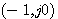 点的包围。为了简便,在我们绘制出开环频率特性以后,不必再转为
点的包围。为了简便,在我们绘制出开环频率特性以后,不必再转为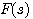 函数,直接使用开环频率特性判断系统是否稳定就可以了。
函数,直接使用开环频率特性判断系统是否稳定就可以了。 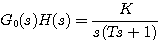

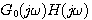 平面上的映射唯一无穷大圆弧段。 本文来自www.eadianqi.com
平面上的映射唯一无穷大圆弧段。 本文来自www.eadianqi.com 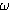 从负无穷大连续变化到正无穷大时,
从负无穷大连续变化到正无穷大时,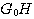 平面上的开环频率特性曲线不包围
平面上的开环频率特性曲线不包围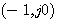 点,否则系统不稳定。若
点,否则系统不稳定。若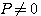 ,闭环系统稳定的充分必要条件是当
,闭环系统稳定的充分必要条件是当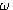 从负无穷大变化到正无穷大时,
从负无穷大变化到正无穷大时,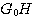 平面上的开环频率特性曲线逆时针方向包围
平面上的开环频率特性曲线逆时针方向包围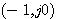 点P周。
点P周。 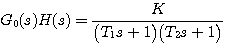

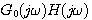 曲线不包围
曲线不包围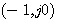 点,所以系统稳定。 本文来自www.eadianqi.com
点,所以系统稳定。 本文来自www.eadianqi.com 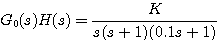


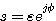
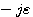 从原点右侧绕到
从原点右侧绕到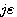 ,当
,当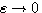 时,该无穷小半圆在开环频率特性上是无穷大半圆弧,如图中虚线所示。 自动控制网www.eadianqi.com版权所有
时,该无穷小半圆在开环频率特性上是无穷大半圆弧,如图中虚线所示。 自动控制网www.eadianqi.com版权所有 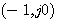 点,而本例中P=0,所以系统稳定。求解特征方程,可得到特征方程的根为
点,而本例中P=0,所以系统稳定。求解特征方程,可得到特征方程的根为 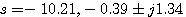 本文来自www.eadianqi.com
本文来自www.eadianqi.com 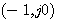 点(顺时针方向,2周)而P=0,根据奈奎斯特判据,系统是不稳定的。求解特征方程可得
点(顺时针方向,2周)而P=0,根据奈奎斯特判据,系统是不稳定的。求解特征方程可得 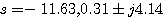
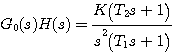 本文来自www.eadianqi.com
本文来自www.eadianqi.com 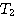 和
和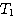 的取值有关。不同情况下的开环频率特性如图4.25所示。
的取值有关。不同情况下的开环频率特性如图4.25所示。 
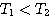 时,开环频率特性不包围
时,开环频率特性不包围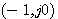 点,系统稳定。
点,系统稳定。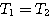 时,开环频率特性正好通过
时,开环频率特性正好通过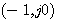 点,说明系统处于临界稳定状态,闭环极点位于虚轴上。
点,说明系统处于临界稳定状态,闭环极点位于虚轴上。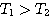 时,开环频率特性顺时针方向包围
时,开环频率特性顺时针方向包围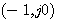 点两周,系统不稳定。 自动控制网www.eadianqi.com版权所有
点两周,系统不稳定。 自动控制网www.eadianqi.com版权所有 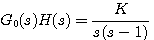 本文来自www.eadianqi.com
本文来自www.eadianqi.com 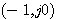 点一周,根据奈奎斯特判据,此系统稳定。 本文来自www.eadianqi.com
点一周,根据奈奎斯特判据,此系统稳定。 本文来自www.eadianqi.com 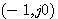 点的方法是假设一个起点在
点的方法是假设一个起点在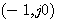 点。矢端在开环频率特性曲线上的矢量。当
点。矢端在开环频率特性曲线上的矢量。当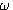 从
从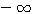 变化到
变化到 时,该矢量的副角变化量与
时,该矢量的副角变化量与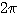 之比即为包围
之比即为包围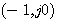 点的周数。
点的周数。 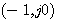 点,系统总是不稳定的。
点,系统总是不稳定的。 
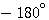 .所以负实轴对应于对数相频特性的
.所以负实轴对应于对数相频特性的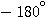 线。 自动控制网www.eadianqi.com版权所有
线。 自动控制网www.eadianqi.com版权所有 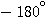 (绝对值大于180),则闭环系统稳定,否则不稳定。
(绝对值大于180),则闭环系统稳定,否则不稳定。  点。继续增大K,开环频率特性曲线仍未包围
点。继续增大K,开环频率特性曲线仍未包围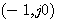 ,系统还是稳定的。但开环频率特性曲线更靠近
,系统还是稳定的。但开环频率特性曲线更靠近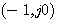 点。我们说它的稳定程度不如前者。再增大K,开环频率特性曲线通过
点。我们说它的稳定程度不如前者。再增大K,开环频率特性曲线通过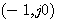 点,系统处于临界稳定状态。随着K的继续增大,开环频率特性曲线包围了
点,系统处于临界稳定状态。随着K的继续增大,开环频率特性曲线包围了 点,系统变成了不稳定系统。图4.27 表明,对于稳定的系统,开环频率特性曲线越靠近
点,系统变成了不稳定系统。图4.27 表明,对于稳定的系统,开环频率特性曲线越靠近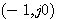 点,系统的稳定程度越低。对于不稳定的系统,开环频率特性曲线离
点,系统的稳定程度越低。对于不稳定的系统,开环频率特性曲线离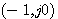 点越远,不稳定程度越大。
点越远,不稳定程度越大。 