|
相平面法是庞加莱1885年首先提出的,本来它是一种求解二元一阶非线性微分方程组的图解法,两个变量构成的直角坐标系称为相平面,方程组的解在相平面上的图象称为相轨迹。 这里是将相平面法用于分析一阶,尤其是二阶非线性控制系统,并形成了一种特定的相平面法,它对研究非线性系统的稳定性、稳定域等基本属性,解释极限环等特殊现象,起到了直观形象的作用。 相平面的基本概念 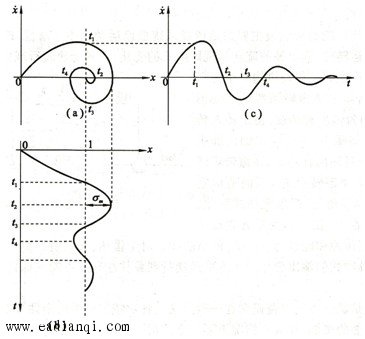 相轨迹曲线 相变量(状态变量) 相平面 相轨迹 相轨迹簇 相平面图 相轨迹绘制的等倾线法 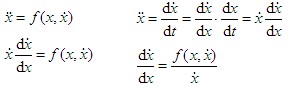 本文来自www.eadianqi.com 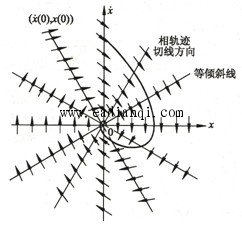 用等倾线法绘制的相轨迹 奇点和奇线 奇点 相平面的奇点 奇点一定位于相平面的横轴上 焦点:当特征根为一对具有负实部的共轭复数根时,奇点为稳定的焦点;当特征根为一对具有正实部的共轭复数根时,奇点为不稳定的焦点。 节点:当特征根为两个负实根时,奇点为稳定的节点;当特征根为两个正实根时,奇点为不稳定的节点。 鞍点:当特征根一个为正实根,一个为负实根时,奇点为鞍点 奇线 特殊的相轨迹——极限环 稳定的极限环: 如果起始于极限环临近范围的内部或外部的相轨迹最终均卷向极限环,则该极限环为稳定的极限环,其内部与外部均为该极限环的稳定区。 稳定的极限环对状态的微小扰动具有稳定性。 系统沿极限环的运动表现为自激振荡。 不稳定的极限环: 如果起始于极限环临近范围的内部或外部的相轨迹最终均卷离极限环,则该极限环为不稳定的极限环。 自动控制网www.eadianqi.com版权所有 不稳定的极限环所表示的周期运动是不稳定的。 不稳定的极限环的临近范围其内部与外部均为该极限环的不稳定区。 半稳定的极限环: 如果起始于极限环临近范围的内部的相轨迹最终均卷向极限环,外部的相轨迹最终均卷离极限环,或者内部的相轨迹最终均卷离极限环,外部的相轨迹最终均卷向极限环,则该极限环为半稳定的极限环。 对于半稳定的极限环,相轨迹均卷向极限环的内部或外部区域为该极限环的稳定区域,相轨迹均卷离极限环的内部或外部区域为该极限环的不稳定区域。 |