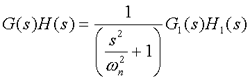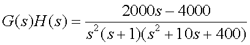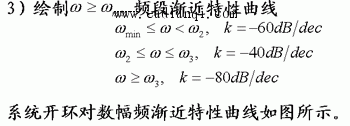4、开环对数频率特性曲线
1、绘制方法
系统开环传递函数作典型环节分解后,先作出各典型环节的对数频率特性曲线,然后采用叠加方法即可方便地绘制系统开环对数频率特性曲线。这里着重介绍开环对数幅频渐近特性曲线的绘制方法。
1)开环传递函数典型环节分解;
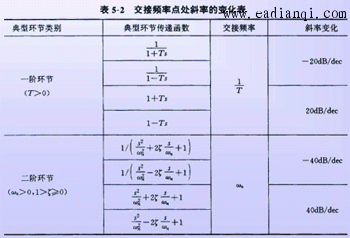
2)确定一阶环节、二阶环节的交接频率,将各交接频率标注在半对数坐标图的ω轴上;
注意:当系统的多个环节具有相同交接频率时,该交接频率点处斜率的变化应为各个环节对应的斜率变化值的代数和。 本文来自www.eadianqi.com
以中=-20vdB/dec的低频渐近线为起始直线,按交接频率由小到大顺序和由表确定斜率变化,再逐一绘制直线。
2、举例说明
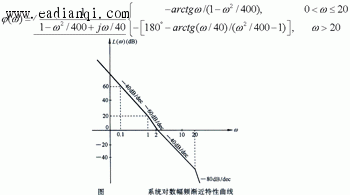
例1 已知系统开环传递函数为 本文来自www.eadianqi.com
试绘制系统开环对数频率特性曲线。
解:开环传递函数的典型环节分解形式为 本文来自www.eadianqi.com
1)确定各交接频率及斜率变化值
非最小相位一阶微分环节:ω2=2,斜率增加20dB/dec
惯性环节:ω1=1,斜率减少20dB/dec
振荡环节:ω3=20,斜率减少40dB/dec
最小交接频率 ωmin=ω1=1 。
2)绘制低频段(ω<ωmin)渐近特性曲线。因为v=2,则低频渐近线斜率k=-40dB/dec,按方法二得直线上一点(ω0,La(ω0))=(1,20dB).
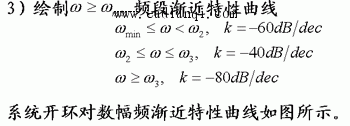
具体计算相角时应注意判别象限。例如在本例中
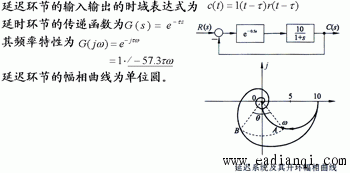
5、延迟环节和延迟系统 本文来自www.eadianqi.com
延时环节:输出量经恒延时后不失真地复现输入量变化的环节。
6、传递函数的频域实验确定
可以运用频率响应实验确定稳定系统的数学模型。
(1)频率响应实验
(2)传递函数确定
从低频段起,将实验所得的对数幅频曲线用斜率为0dB/dec,+/-dB/dec,+/-dB/dec,...等直线分段近似,获得对数幅频渐近特性曲线。
下面举例说明其方法和步骤。
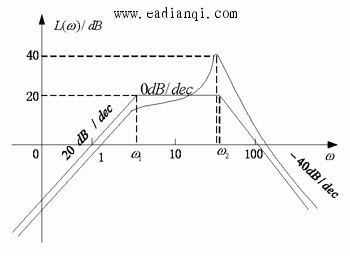
例 某最小相位系统由频率响应实验获得的对数幅频曲线如图所示,试确定其传递函数。
自动控制网www.eadianqi.com版权所有
解:1)确定系统积分或微分环节的个数。由于对数幅频特性低频渐近线的斜率为-20vdB/dec,而图5-27中低频渐近线的斜率为+20dB/dec,故有v =-1,系统含有一个微分环节。
2)确定系统传递函数表达式。由于对数幅频特性渐近线为分段折线,其转折点分别对应系统所含典型环节的交接频率,每个交接频率处的斜率变化决定了典型环节的种类。图中在ω处,斜率变化为-20dB/dec,对应惯性环节;在ω处,斜率变化为-40dB/dec,且存在谐振,对应振荡环节。
|
|