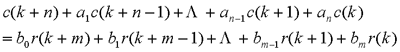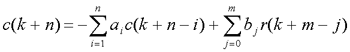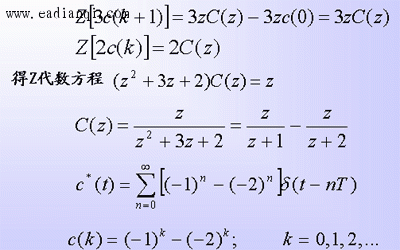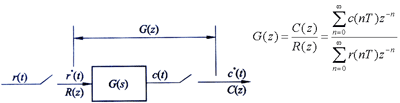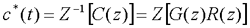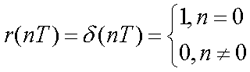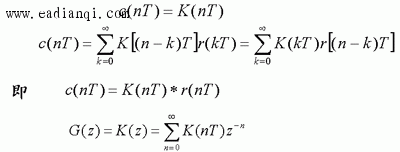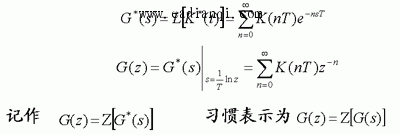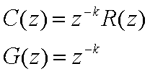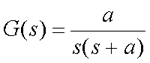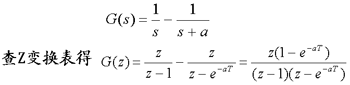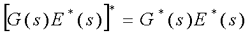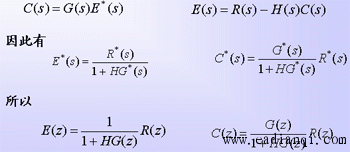|
1、离散系统的数学定义 将输入序列r(n),n=0,+/-1,+/-2,A, 变换为输出序列c(n)的一种变换关系,称为离散系统。记作c(n=F[r(n)]) 如果上式所示的变换关系是线性的,则称为线性离散系统; 如果这种变换关系是非线性的,则称为非线性离散系统。 ⑴线性离散系统 如果离散系统满足叠加原理,则称为线性离散系统,即有如下关系式
⑵线性定常离散系统
⑴ 迭代法 若已知差分方程,并且给定输出序列的初值,则可以利用递推关系,在计算机上一步一步地算出输出序列。 自动控制网www.eadianqi.com版权所有 例7-16 已知差分方程 c(k)=r(k)+5c(k-1)-6c(k-2)输入序列r(k)=1,初始条件为c(0)=0,c(1)=1 ,试用迭代法求输出序列c(k),k=0,1,2,A,10。 解 根据初始条件及递推关系,得 C(0)=0 C(1)=1 C(2)=r(2)+5c(1)-6c(0)=6 C(3)=r(3)+5c(2)-6c(1)=25 C(4)=r(4)+5c(3)-6c(2)=90 C(5)=r(5)+5c(4)-6c(3)=301 C(6)=r(6)+5c(5)-6c(4)=966 C(7)=r(7)+5c(6)-6c(5)=3025 C(8)=r(8)+5c(7)-6c(6)=9330 C(9)=r(9)+5c(9)-6c(8)=86526 ⑵ Z变换法 利用Z变换的实数位移定理,得到以Z为变量的代数方程,然后对代数方程的解C(z)取Z反变换,求得输出序列c(k)。 例 试用变换法解下列二阶差分方程
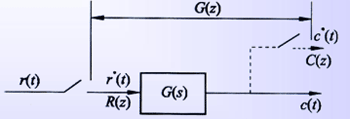
⑴ 脉冲传递函数定义 设开环离散系统如下图所示,线性定常离散系统的脉冲传递函数定义为系统的初始条件为零时系统输出采样信号的Z变换与输入采样信号的Z变换之比,记作
⑵ 脉冲传递函数意义 输入单位序列:
自动控制网www.eadianqi.com版权所有 ⑶ 脉冲传递函数求法 连续系统或元件的脉冲传递函数G(z) ,可以通过其传递函数G(s)来求取。
解 对差分方程取Z变换,并由实数位移定理得
例7-19 设图7-23所示开环系统中的
解 将G(s)展成部分分式
⑴采样拉氏变换的两个重要性质 1)采样函数的拉氏变换具有周期性,即
自动控制网www.eadianqi.com版权所有 2)若采样函数的拉氏变换E*(s)与连续函数的拉氏变换G(s)相乘后再离散化,则E*(s)可以从离散符号中提出来,即
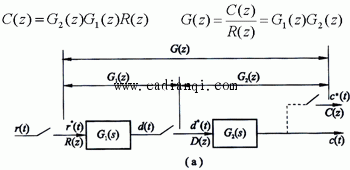
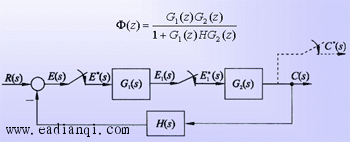
1)串联环节之间有采样开关 设开环离散系统如图(a)所示,由图可得 D(z)=G1(z)R(z) c(z)=G2(z)D(z) 于是有
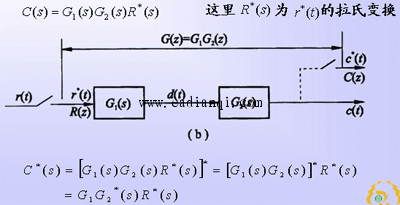
2)串联环节之间无采样开关 设开环离散系统如图 (b)所示,显然
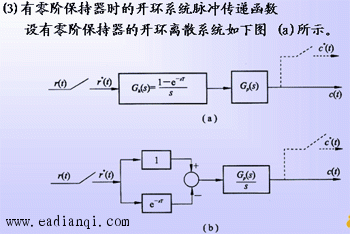
自动控制网www.eadianqi.com版权所有 在串联环节之间有无同路不采样开关隔离时,其总的脉冲传递函数和输出Z变换是不相同的。但是,不同之处仅表现在其零点不同,极点仍然一样。这也是离散系统特有的现象。 ⑶ 有零阶保持器时的开环系统脉冲传递函数设有零阶保持器的开环离散系统如下图 (a)所示。
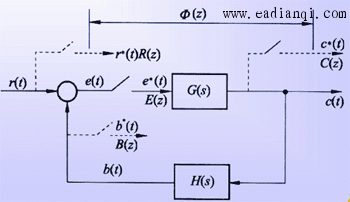
下图是一种比较常见的误差采样闭环离散系统结构图。
φ(z)≠Z[φ(s)] φe(z)≠Z[φe(s)] 这是由于采样器在闭环系统中有多种配置之故。 例 设闭环离散系统结构图所示,试证其闭环脉冲传递函数为
本文来自www.eadianqi.com ⑴变换法的局限性 ⑵修正变换法 |