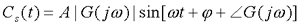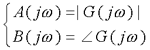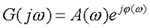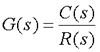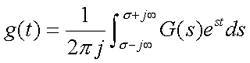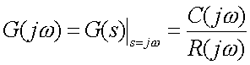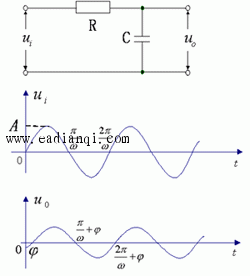
频率特性的基本概念

(1)、RC网络
左图为RC滤波网络，设电容C的初始电压为U0，取输入信号为正弦信号Ui=Asinωt，曲线如图所示。当响应呈稳态时，可以看出仍为正弦信号，频率与输入信号相同，幅值较输入信号有一定衰减，相位存在一定延迟。

(2) 、频率特性定义
设稳定线性定常系统的传函为

本文来自www.eadianqi.com

输出响应稳态分量的拉氏反变换为

上面各式比较，可知

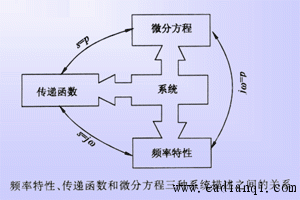
    上面表明，由谐波输入产生的输出稳态分量仍然是与输入同频率的谐波函数，幅值和相位的变化是同频率的函数，且与系统数学模型相关。
    频率特性
    定义谐波输入下，输出响应中与输入同频率的谐波分量与谐波输入的幅值之比A(ω) 为幅频特性，相位之差ψ(ω)为相频特性，并称其指数表达形式

为系统的频率特性。
频率特性也是系统数学模型的一种表达形式。频率特性的定义既可以适用于稳定系统，也可适用于不稳定系统。稳定系统的频率特性可以用实验方法确定。
线性定常系统的传递函数为零初始条件下，输出和输入的拉氏变换之比自动控制网www.eadianqi.com版权所有

上式的拉氏反变换为

本文来自www.eadianqi.com

    频率特性的物理意义：稳定系统的频率特性等于输出和输入的傅氏变化之比，这就是频率特性的物理意义。

    (3)、三种系统描述之间的关系
    由于频率特性是传递函数的一种特殊形式，因而它和传递函数、微分方程一样，可以表征系统的运动规律，是描述系统的又一种数学模型。