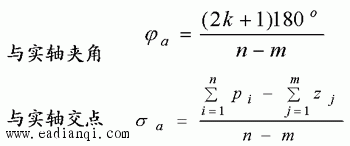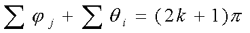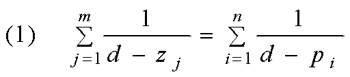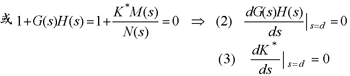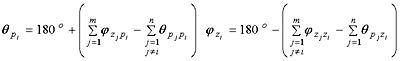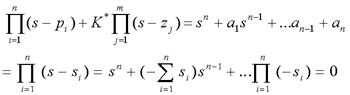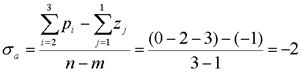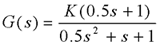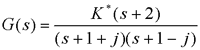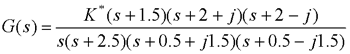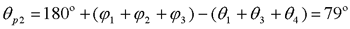|
本文讨论绘制概略根轨迹的基本法则和闭环极点的确定方法。 在下面的讨论中,假定所研究的变化参数是根轨迹增值K*,当可变参数为系统的其它参数时,这些基本法则仍然适用。应当指出的是,用这些基本法则绘出的根轨迹,其相角遵循条件180°+2kπ ,因此称为180°根轨迹,相应的绘制法则也就可以叫做180°根轨迹的绘制法则。 1 根轨迹绘制基本法则 法则1 根轨迹的起点和终点。根轨迹起始于开环极点,终止于开环零点。
法则2
法则3
法则4 本文来自www.eadianqi.com
根轨迹分离点 两条或两条以上的根轨迹分支在 s 平面上相遇又立即分开的点称为分离点(会合点)。 分离点的坐标 d 由下列方程所决定:
(2)若实轴上的根轨迹的左右两侧均为开环零点(包括无限零点)或开环极点(包括无限极点),则在此段根轨迹上必有分离点。 本文来自www.eadianqi.com (3)分离点若在复平面上,则一定是成对出现的。
法则6 根轨迹的起始角和终止角 起始角:根轨迹离开复平面上开环极点处的切线与实轴的夹角θpi 终止角:根轨迹进入复平面上开环零点处的切线与实轴的夹角Ψzi 。
法则7 根轨迹与虚轴的交点 交点对应的根轨迹增益K*和角频率ω可以用劳斯判据或令闭环特征方程中的s=jω,然后分别令其实部和虚部为零来确定。 本文来自www.eadianqi.com 实际上若根轨迹与虚轴相交,则表示闭环系统存在纯虚根,这意味着的数值使闭环系统处于临界稳定状态。 法则8 根之和 系统的闭环特征方程在n>m的一般情况下,可以有不同形式的表示
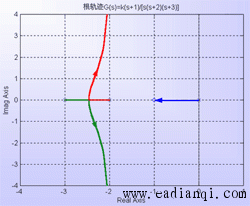
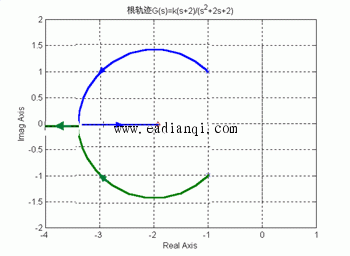
2、根轨迹法则应用举例 例 设系统结构图与开环零、极点分布如图所示,试绘制其概略根轨迹。
自动控制网www.eadianqi.com版权所有 解:由法则4,实轴上区域和是根轨迹,在图中以粗实线表示。 由法则2,该系统有三条根轨迹分支,且对称于实轴。 由法则1,一条根轨迹分支起于开环极点,终于开环有限零点,另外两条根轨迹分支起于开环极点和,终于无穷远处(无限零点)。 由法则3,两条终于无穷的根轨迹的渐近线与实轴交角为90°和 270°,交点坐标为
自动控制网www.eadianqi.com版权所有 解:首先将G(s)写成零、极点标准形式
解:将开环零、极点画在后面图中。按如下典型步骤 本文来自www.eadianqi.com 1)确定实轴上的根轨迹。本例实轴上区域[0,1.5]和[-2.5,-∞]为轨迹。 2)确定根轨迹的渐近线。本例n=4,m=3,故只有一条180°的渐近线。 3)确定分离点。本例无分离点。 4)确定起始角与终止角。根轨迹在极点(-0.5+1.5)处的起始角为
|