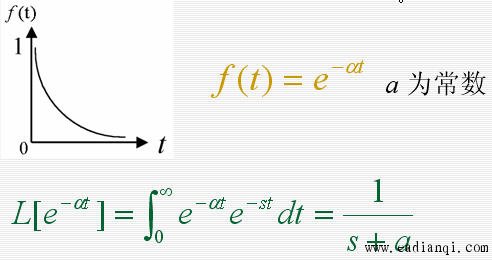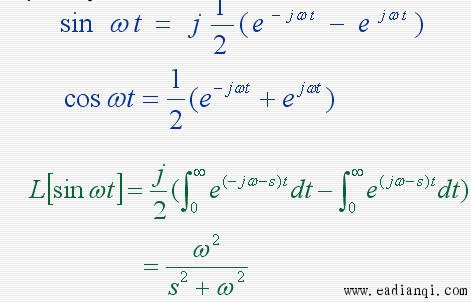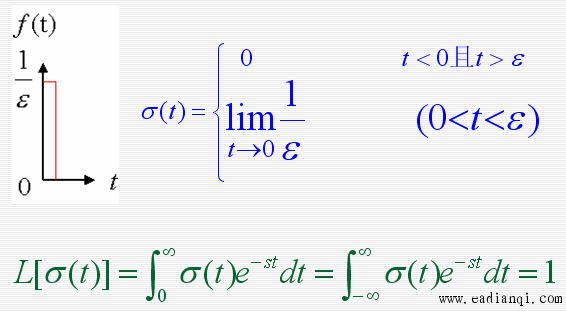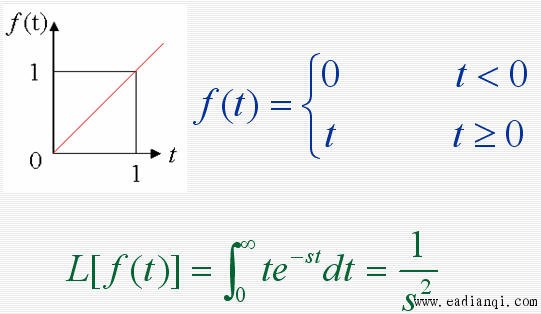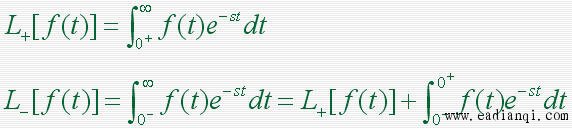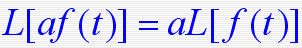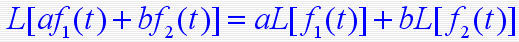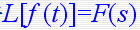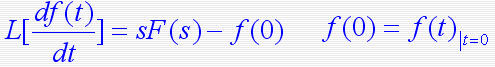|
1. 拉氏变换 设函数 f ( t ) 在任一有限区间上分段连续,且存在一正实数s,使得: 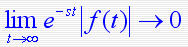 则函数 f ( t ) 的拉普拉斯变换存在,并定义为 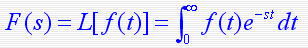 F(s)称为函数 f ( t ) 的拉普拉斯变换或象函数,它是一个复变函数, f ( t ) 称为F(s)的原函数。 2. 拉氏逆变换 若F(s)是 f ( t ) 的拉氏变换,则称f ( t )为 F(s)的拉氏逆变换(原象函数) 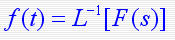 3. 几种典型函数的拉氏变换 1)单位阶跃函数 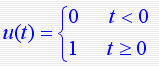  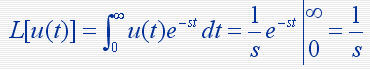 2)指数函数
本文来自www.eadianqi.com 当 f (t) 及其各阶导数在t=0时刻的值均为零时 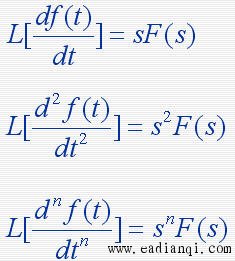 3)复微分定理 若L[ f (t) ]=F(s),则除F(s)的极点外,有: 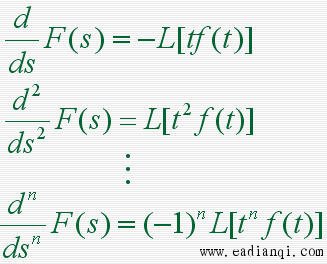 4)延迟定理 当t<0时,f (t)=0 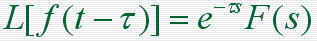 5)位移定理 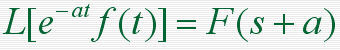 6)初值定理 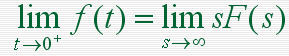 7)终值定理 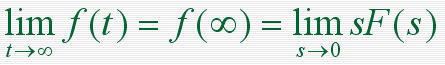 8)卷积定理  9)时间比例尺的改变 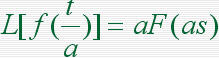 自动控制网www.eadianqi.com版权所有
|