|
在进行两相同步旋转坐标变换时,只规定了d,q两轴的相互垂直关系和与定子频率同步的旋转速度,并未规定两轴与电机旋转磁场的相对位置,对此是有选择余地的。
按转子磁链定向
现在d轴是沿着转子总磁链矢量的方向,并称之为 M(Magnetization)轴,而 q 轴再逆时针转90°,即垂直于转子总磁链矢量,称之为 T(Torque)轴。
这样的两相同步旋转坐标系就具体规定为 M,T 坐标系,即按转子磁链定向(Field Orientation)的坐标系。
当两相同步旋转坐标系按转子磁链定向时,应有 自动控制网www.eadianqi.com版权所有
|
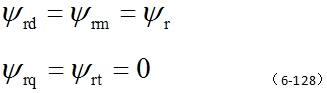 |
按转子磁链定向后的系统模型
代入转矩方程式(6-113)和状态方程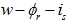 中并用m,t替代d,q,即得 中并用m,t替代d,q,即得 |
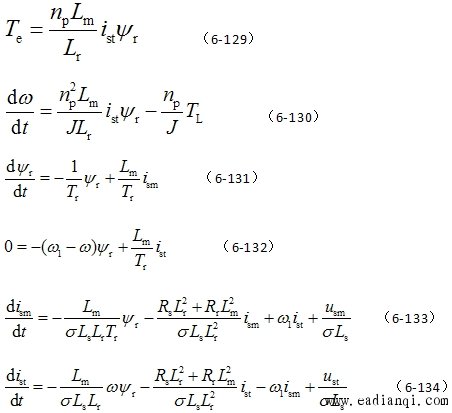 |
|
由于,状态方程中的式(6-132)蜕化为代数方程,整理后得转差公式 |
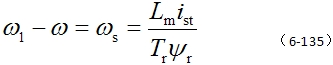 |
|
这使状态方程降低了一阶。 自动控制网www.eadianqi.com版权所有
由式(6-131)可得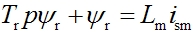 本文来自www.eadianqi.com 本文来自www.eadianqi.com
|
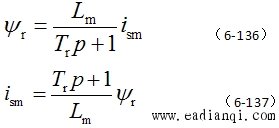 |
|
按转子磁链定向的意义
式(6-136)或式(6-137)表明,转子磁链仅由定子电流励磁分量产生,与转矩分量无关,从这个意义上看,定子电流的励磁分量与转矩分量是解耦的。
式(6-136)还表明,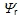 与 与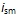 之间的传递函数是 一阶惯性环节,时间常数为转子磁链励磁时间常数,当励磁电流分量 之间的传递函数是 一阶惯性环节,时间常数为转子磁链励磁时间常数,当励磁电流分量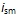 突变时, 突变时,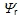 的变化要受到励磁惯性的阻挠,这和直流电机励磁绕组的惯性作用是一致的。 自动控制网www.eadianqi.com版权所有 的变化要受到励磁惯性的阻挠,这和直流电机励磁绕组的惯性作用是一致的。 自动控制网www.eadianqi.com版权所有
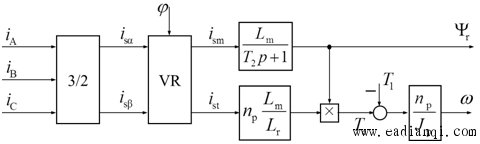
式(6-136)或(6-137)、(6-135)和(6-129)构成矢量控制基本方程式,按照这些关系可将异步电机的数学模型绘成图6-54中的形式,图中前述的等效直流电机模型(见图6-52)被分解成 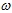 和 和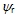 两个子系统。可以看出,虽然通过矢量变换,将定子电流解耦成 两个子系统。可以看出,虽然通过矢量变换,将定子电流解耦成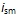 和 和 两个分量,但是,从 两个分量,但是,从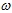 和 和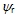 两个子系统来看,由于 两个子系统来看,由于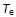 同时受到 同时受到 和 和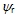 的影响,两个子系统仍旧是耦合着的。 的影响,两个子系统仍旧是耦合着的。 自动控制网www.eadianqi.com版权所有
电流解耦数学模型的结构 自动控制网www.eadianqi.com版权所有
|
 |
|
图6-54 异步电动机矢量变换与电流解耦数学模型 |
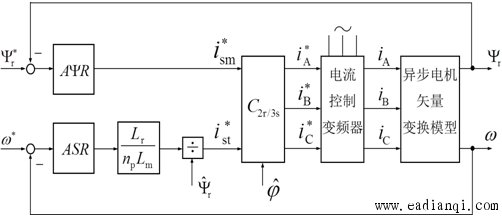
按照图6-53的矢量控制系统原理结构图模仿直流调速系统进行控制时,可设置磁链调节器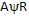 和转速调节器ASR分别控制 和转速调节器ASR分别控制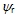 和 和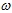 ,如图6-55所示。 ,如图6-55所示。
为了使两个子系统完全解耦,除了坐标变换以外,还应设法抵消转子磁链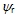 对电磁转矩 对电磁转矩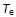 的影响。 的影响。 本文来自www.eadianqi.com
矢量控制系统原理结构图图6-55 |
 |
|
比较直观的办法是,把ASR的输出信号除以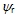 ,当控制器的坐标反变换与电机中的坐标变换对消,且变频器的滞后作用可以忽略时,此处的( ,当控制器的坐标反变换与电机中的坐标变换对消,且变频器的滞后作用可以忽略时,此处的(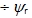 )便可与电机模型中的( )便可与电机模型中的(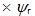 )对消,两个子系统就完全解耦了。这时,带除法环节的矢量控制系统可以看成是两个独立的线性子系统,可以采用经典控制理论的单变量线性系统综合方法或相应的工程设计方法来设计两个调节器 )对消,两个子系统就完全解耦了。这时,带除法环节的矢量控制系统可以看成是两个独立的线性子系统,可以采用经典控制理论的单变量线性系统综合方法或相应的工程设计方法来设计两个调节器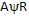 和ASR。 和ASR。 自动控制网www.eadianqi.com版权所有
解耦条件
因此,两个子系统完全解耦只有在下述三个假定条件下才能成立:
①转子磁链的计算值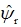 等于其实际值 等于其实际值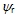 ; ;
②转子磁场定向角的计算值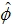 等于其实际值 等于其实际值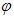 ; ;
③忽略电流控制变频器的滞后作用。 自动控制网www.eadianqi.com版权所有
|