1.定义
    正向规则演绎系统是从事实到目标进行操作的,也就是从if到then的方向进行推理的。 本文来自www.eadianqi.com

2.正向推理过程
    (1) 事实表达式的与或形变换把事实表示为非蕴涵形式的与或形,作为系统的总数据库。具体变换步骤与前述化为子句形类似。
    注意:我们不想把这些事实化为子句形,而是把它们表示为谓词演算公式,并把这些公式变换为叫做与或形的非蕴涵形式。
    例:有事实表达式
        (u)(v){Q(v,u)∧～[(R(v)∨P(v))∧S(u,v)]}
    把它化为
        Q(v,A)∧{[～R(v)∧～P(v)]∨～S(A,v)}
    对变量更名标准化,使得同一变量不出现在事实表达式的不同主要合取式中,得:
        Q(w,A)∧{[～R(v)∧～P(v)]∨～S(A,v)}
    (2) 事实表达式的与或图表示
    将上例与或形的事实表达式用与或图来表示,见图1。 自动控制网www.eadianqi.com版权所有

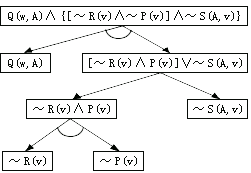
图1 一个事实表达式的与或树表示 本文来自www.eadianqi.com

    一般把事实表达式的与或图表示倒过来画,即把根节点画在最下面,而把其后继节点往上画。上节的与或图表示,就是按通常方式画出的,即目标在上面。
    (3) 与或图的F规则变换
    这些规则是建立在某个问题辖域中普通陈述性知识的蕴涵公式基础上的。把允许用作规则的公式类型限制为下列形式:
        L=>W
    式中:L是单文字;W为与或形的唯一公式。
    将这类规则应用于与或图进行推演。假设有一条规则L=>W,根据此规则及事实表达式F(L),可以推出表达式F(W),产生一个含有F(W)表示的新图。该过程以极其有效的方式达到了用其它方法要进行多次消解才能达到的目的。
    (4) 作为终止条件的目标公式
    应用F规则的目的在于从某个事实公式和某个规则集出发来证明某个目标公式。在正向推理系统中,这种目标表达式只限于可证明的表达式,尤其是可证明的文字析取形的目标公式表达式。用文字集表示此目标公式,并设该集各元都为析取关系。

自动控制网www.eadianqi.com版权所有