|
微分性质 自动控制网www.eadianqi.com版权所有
积分性质
证明:因为 自动控制网www.eadianqi.com版权所有
所以 这是一个特别重要的性质,因为它将时域内的微分用频域内乘以j所代替。在后面讨论利用傅里叶变换来分析由微分方程描述的LTI系统时,这一性质极其有用。 本文来自www.eadianqi.com 例3.6.2 求单位阶跃函数x(t)=u(t)的傅里叶变换。 本文来自www.eadianqi.com 解:已知单位冲激函数的傅里叶变换: 本文来自www.eadianqi.com  根据单位阶跃函数和单位冲激函数之间的关系: 本文来自www.eadianqi.com 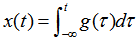 对上式取傅里叶变换,利用积分性质,得: 本文来自www.eadianqi.com 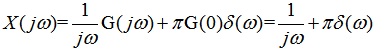 例3.6.3 现在求图示3-6-2(a)信号x(t)的傅里叶变换. 自动控制网www.eadianqi.com版权所有
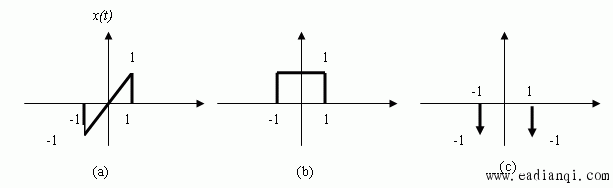
思路:我们不直接对x(t)应用傅里叶变换式求解 首先,对x(t)求微分得g(t): 自动控制网www.eadianqi.com版权所有 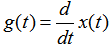 g(t)就是一个矩形脉冲和两个冲激函数的和,如图(b)和(c)。g(t)的傅里叶变换为 本文来自www.eadianqi.com 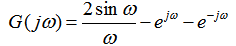 利用傅里叶积分性质,得 自动控制网www.eadianqi.com版权所有 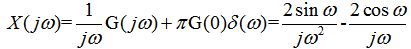 小结:这节课我们学习了傅里叶变换的线性、时移性质、共轭和共轭对称性以及微分和积分性质,大家要掌握这些性质的应用。 自动控制网www.eadianqi.com版权所有 |
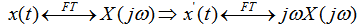
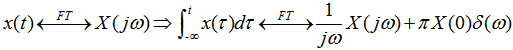 本文来自www.eadianqi.com
本文来自www.eadianqi.com 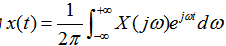
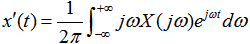
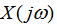 ,而是考虑利傅里叶变换的性质。 自动控制网www.eadianqi.com版权所有
,而是考虑利傅里叶变换的性质。 自动控制网www.eadianqi.com版权所有