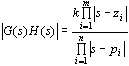|
基于系统稳定的充要条件，反馈系统的稳定性由其闭环极点唯一确定。反馈系统的闭环极点就是该系统特征方程的根。一般来说，当特征方程的阶数较高时，求根过程是很复杂的，特别是在系统参数变化情况下求根，更是需要进行大量的运算，而且还不宜直观看出参数变化对系统闭环极点分布的影响。对此，伊凡思(W.R.Evans)提出了一种图解反馈系统特征方程的工程方法，该法称为根轨迹法。 本文来自www.eadianqi.com 反馈系统根轨迹的有关概念 自动控制网www.eadianqi.com版权所有
根轨迹方程 自动控制网www.eadianqi.com版权所有
设反馈系统的特征方程为 自动控制网www.eadianqi.com版权所有
式中
应用上述根轨迹方程绘制反馈系统根轨迹前，还需将开环传递函数
式中 自动控制网www.eadianqi.com版权所有
绘制根轨迹的条件 自动控制网www.eadianqi.com版权所有 由负反馈系统根轨迹方程可得 自动控制网www.eadianqi.com版权所有
或 由正反馈系统的根轨迹方程得 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
或 由上可知,180°根轨迹和0°根轨迹的幅值条件相同，而相角条件是有别的。 自动控制网www.eadianqi.com版权所有
本文来自www.eadianqi.com
幅值、相角的计算 自动控制网www.eadianqi.com版权所有
设系统开环传递函数具有标准形式 本文来自www.eadianqi.com
本文来自www.eadianqi.com
上面两个等式分别为幅值、相角的计算公式。 本文来自www.eadianqi.com
本文来自www.eadianqi.com
本文来自www.eadianqi.com
1、绘制反馈系统的根轨迹（包括180°根轨迹和0°根轨迹）只须依据相角条件，而幅值条件则用于计算根轨迹上某确定点
2、参变量 自动控制网www.eadianqi.com版权所有 |
根轨迹法是在已知反馈系统的开环极点与零点分布基础上，通过系统参数变化图解特征方程，即
是反馈系统前向通道的传递函数；
是反馈系统反馈通道的传递函数；
是反馈系统的开环传递函数；
对应负反馈系统；
对应正反馈系统。则
为绘制负反馈系统的根轨迹方程，
为绘制正反馈系统的根轨迹方程。 
如下标准形式 
为绘制根轨迹的可变参数，称参变量或根轨迹增益，取值范围为
.
为系统的开环极点。
为系统的开环零点。 
自动控制网www.eadianqi.com版权所有 
即为绘制负反馈系统根轨迹的幅值条件；
则构成绘制负反馈系统根轨迹的相角条件，负反馈系统的根轨迹又称作180°根轨迹或常规根轨迹。 
即为绘制正反馈系统根轨迹的幅值条件，
则是绘制正反馈系统根轨迹的相角条件。正反馈系统的根轨迹又称作0°根轨迹。 本文来自www.eadianqi.com 
自动控制网www.eadianqi.com版权所有 
两点说明 
并非一定为系统的开环增益，如参变量
为系统开环增益或与之成比例，则此类根轨迹称