|
一、标注开环极点和零点,纵横坐标用相同的比例尺; 二、实轴上的根轨迹; 三、n-m条渐近线; 四、根轨迹的出射角,入射角; 五、根轨迹与虚轴的交点; 六、根轨迹的分离点,会合点; 结合根轨迹的连续性,对称性,根轨迹的支数,起始点和终 点,闭环极点之和及之积等性质画出根轨迹. 例1 已知系统结构图如图所示，试作多回路系统的根轨迹。 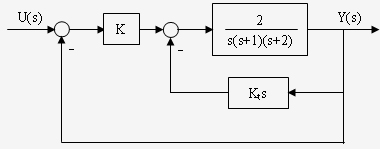 图1 多回路系统结构图 解: 在一般情况下，绘制多回路系统的根轨迹时，首先根据内反馈回路的开环传递函数，绘制内反馈回路的根轨迹，确定内反馈回路的极点分布。然后由内反馈回路的零、极点和内回路外的零、极点构成整个多回路系统的开环零、极点。再按照单回路根轨迹的基本法则，绘制总的系统的根轨迹。 自动控制网www.eadianqi.com版权所有 需要指出，这样绘制出来的根轨迹只能确定多回路系统极点的分布，而多回路系统的零点还需要根据多回路系统闭环传递函数来确定。 下面根据图所示系统，绘制多回路系统的根轨迹。 首先确定内回路的根轨迹。 内回路闭环传递函  内回路特征方程  作 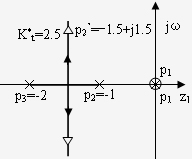 由0 时的根轨迹，需要根据内回路特征方程 ，构造一个新系统，使新系统的特征方程与 一样，而参数 应相当于开环增益，故新系统的开环传递函数应为  式中 ,内回路开环有三个极点 、 、 一个零点 .
 本文来自www.eadianqi.com 图4-2 内回路根轨迹 在绘制根轨迹时，开环传递函数的分子分母中若有相同因子时，不能相消，相消后将会丢掉闭环极点。而实际上我们将一对靠得很近的闭环零、极点称为偶极子。偶极子这个概念对控制系统的综合设计是很有用的，我们可以有意识地在系统中加入适当的零点，以抵消对动态过程影响较大的不利极点，使系统的动态过程获得改善。工程上，某极点  与某零点 之间的距离比它们的模值小一个数量级，就可认为这对零极点为偶极子。内回路当  由0 时的根轨迹见图4-6所示。当 =2.5， 时，对应的内回路闭环极点分别为 、   本文来自www.eadianqi.com 内回路闭环零、极点确定后，再画K由  的多回路系统根轨迹。多回路系统的开环传递函数应为   1、整个负实轴为根轨迹段 2、渐近线  {60°、180°、-60°}  自动控制网www.eadianqi.com版权所有 3、起始角  －135°－90°取  ， －45°  ， 45° 4、求与虚轴的交点  令  代入得 :  ， ,  ， 本文来自www.eadianqi.com 多回路系统根轨迹见图4-3所示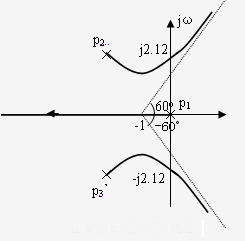：  图 4-3 多回路系统根轨  取1.25， 时，此多回路系统将有两个闭环极点分布在s平面的右半部，系统变图4-3多回路系统根轨迹为不稳定。
|