|
在理论上,扰动作用下的稳态误差的分析方法与输入作用下的分析方法相同,即在理论上将扰动信号看作是另一个输入信号。
要点:扰动误差传递函数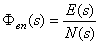 ; ;
因为系统对扰动信号响应期望值为零,则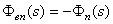
*响应输入信号的误差系统型别:据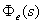 讨论; 讨论;
*响应扰动信号的误差系统型别:据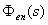 讨论; 讨论;
响应扰动信号的系统型别: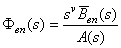 ; ; 自动控制网www.eadianqi.com版权所有
响应扰动信号的稳态误差级数: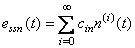 。 自动控制网www.eadianqi.com版权所有 。 自动控制网www.eadianqi.com版权所有
例1 已知系统方框图如右图 所示。输入信号r(t)=t·1,扰动信号n(t)=-1,计算该系统的稳态误差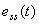 。 本文来自www.eadianqi.com 。 本文来自www.eadianqi.com
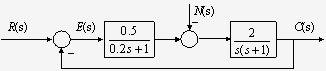 本文来自www.eadianqi.com
解:误差传递函数: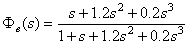 , 自动控制网www.eadianqi.com版权所有 , 自动控制网www.eadianqi.com版权所有
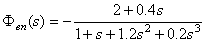 ; ;
信号的各阶导数: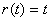 ; ; ; ;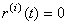 , ,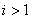 ; ;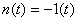 , ,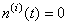 , ,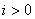 。 自动控制网www.eadianqi.com版权所有 。 自动控制网www.eadianqi.com版权所有
动态误差系数: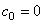 , ,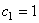 ; ;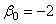 ; ;
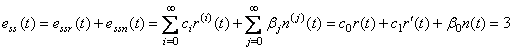
由误差传递函数知,该系统是响应输入的Ⅰ型系统,响应扰动信号的0型系统。 自动控制网www.eadianqi.com版权所有
例2 已知系统框图及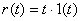 , ,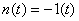 ;计算该系统的稳态误差。 本文来自www.eadianqi.com ;计算该系统的稳态误差。 本文来自www.eadianqi.com
解: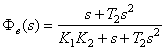 , ,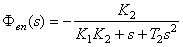 ; ; 自动控制网www.eadianqi.com版权所有
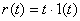 , ,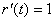 , ,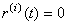 , ,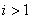 ; ;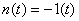 , ,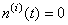 , ,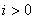 ; ;
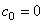 , ,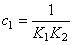 ; ;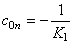 , ,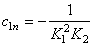 ; 自动控制网www.eadianqi.com版权所有 ; 自动控制网www.eadianqi.com版权所有
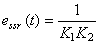 ; ;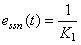 ; 自动控制网www.eadianqi.com版权所有 ; 自动控制网www.eadianqi.com版权所有
例3 已知系统框图及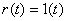 , ,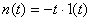 ;计算该系统的稳态误差。 自动控制网www.eadianqi.com版权所有 ;计算该系统的稳态误差。 自动控制网www.eadianqi.com版权所有
解: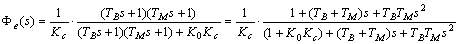 自动控制网www.eadianqi.com版权所有
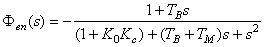 ; ;
 , ,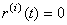 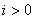 ; ;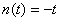 , ,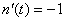 , ,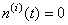 , ,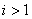 ; ;
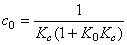 ; ;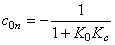 , ,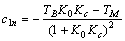 ; 自动控制网www.eadianqi.com版权所有 ; 自动控制网www.eadianqi.com版权所有
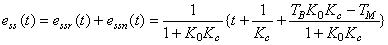 。 。
该系统的稳态误差是随时间变化的线性函数。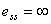 。 本文来自www.eadianqi.com 。 本文来自www.eadianqi.com
|

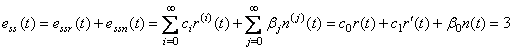
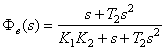 ,
,