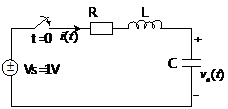微分方程是控制系统模型的基础，一般来讲，利用机械学电学力学等物理规律，便可以得到控制系统的动态方程，这些方程对于线性定常连续系统而言是一种常系数的线性微分方程。 自动控制网www.eadianqi.com版权所有

    如果已知输入量及变量的初始条件，对微分方程进行求解，就可以得到系统输出量的表达式，并由此对系统进行性能分析。 本文来自www.eadianqi.com

    通过拉氏变换和反变换，可以得到线性定常系统的解析解，这种方法通常只适用于常系数的线性微分方程，解析解是精确的，然而通常寻找解析解是困难的。MATLAB提供了ode2（三）ode45等微分方程的数值解法函数，不仅适用于线性定常系统，也适用于非线性及时变系统。

自动控制网www.eadianqi.com版权所有

本文来自www.eadianqi.com

    电路图如下，R=1.4欧，L=2亨，C=0.32法，初始状态：电感电流为零，电容电压为0.5V，t=0时刻接入1V的电压，求0

本文来自www.eadianqi.com

本文来自www.eadianqi.com

    例exp3_1．m 本文来自www.eadianqi.com

    clear 本文来自www.eadianqi.com

    clc

本文来自www.eadianqi.com

    close 本文来自www.eadianqi.com

    t0=0; 自动控制网www.eadianqi.com版权所有

    tfinal=15;

    x0=[0.5;0];%初始化，电感电流为0，电容电压为0.5v 自动控制网www.eadianqi.com版权所有

    %tol=0．001;%数值计算精度 自动控制网www.eadianqi.com版权所有

    [t,x]=ode45('elecsys',t0,tfinal,x0);

自动控制网www.eadianqi.com版权所有

    %elecsys是系统微分方程的描述函数

自动控制网www.eadianqi.com版权所有

    figure(1) 本文来自www.eadianqi.com

    subplot(211)

    plot(t,x(:,1)) 自动控制网www.eadianqi.com版权所有

    title('capacitorvoltage')

    xlabel('time-sec')

    subplot(212)

    plot(t,x(:,2))

    title('currentofL')

本文来自www.eadianqi.com

    xlabel('time-sec')

自动控制网www.eadianqi.com版权所有

    figure(2) 本文来自www.eadianqi.com

    vc=x(:,1); 自动控制网www.eadianqi.com版权所有

    i=x(:,2);

自动控制网www.eadianqi.com版权所有

    plot(vc,i);

    title('currentversuscapacitorvoltage')

    xlabel('capacitorvoltage') 本文来自www.eadianqi.com

    ylabel('current') 自动控制网www.eadianqi.com版权所有